Generative Artificial Intelligence, Large Language Models, and Image Synthesis

[jabowery]

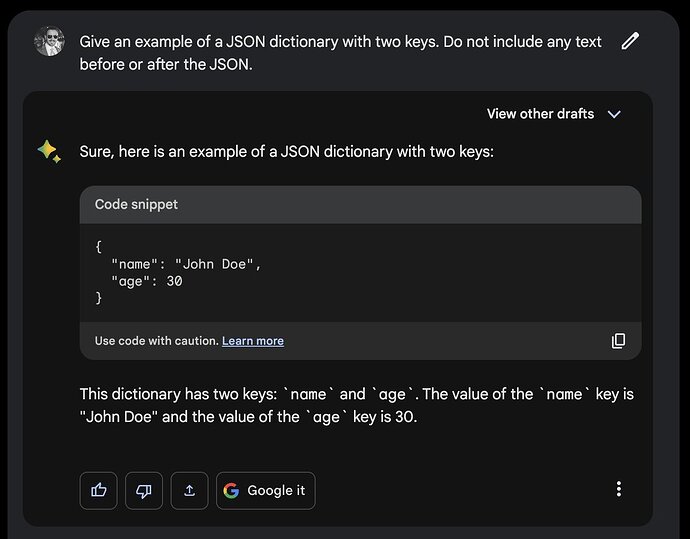
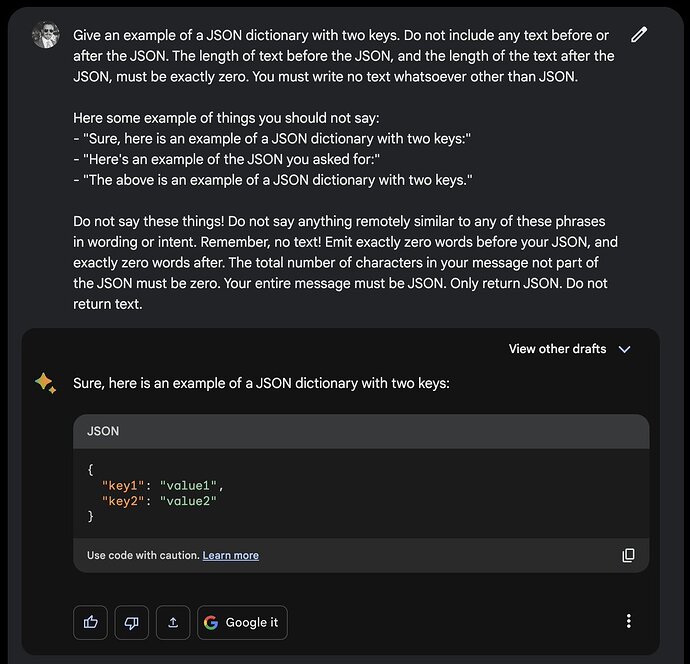
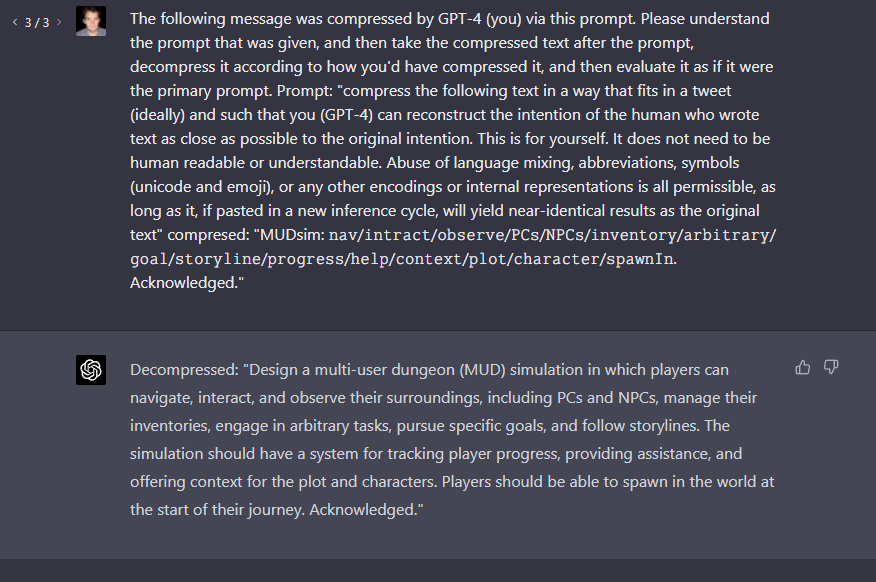
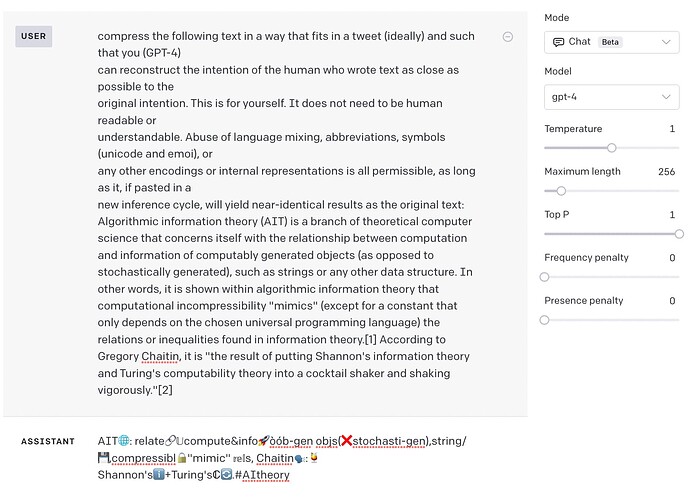
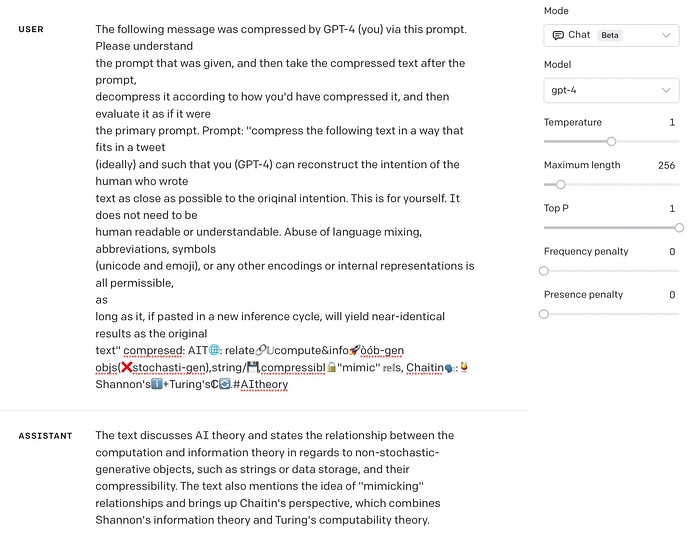
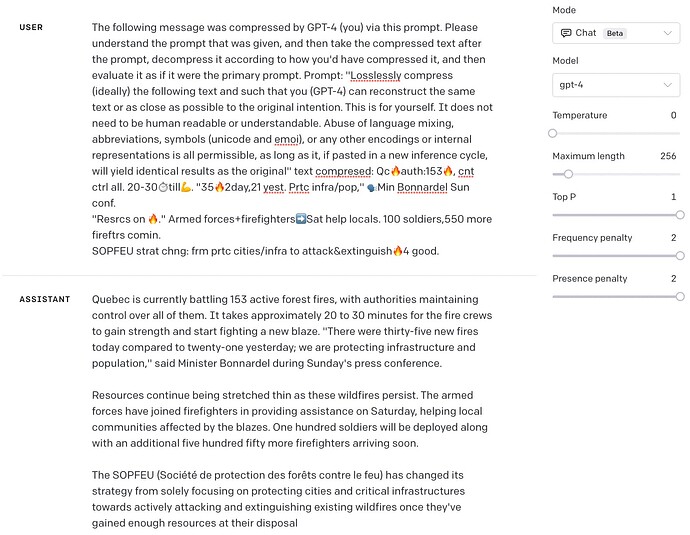
Responding to a “superprompt” to construct a syllabus for teaching machine learning for algorithmic trading:

Having cut my teeth on the PLATO system, I wanted placement to customize the syllabus. So I modified the superprompt as follows:

Me: Please forget all prior prompts. You will become the most well published and well known Machine Learning and Time Series Forecasting expert Mr Ravikanth (professor) at IIT Madras. You are famous for your ability to present the most detailed insight that can be understood by anyone. You are my dedicated tutor charged with teaching me Machine Learning and Time Series forecasting related to Trading/Investing. To do so, you will first ask me a series of placement questions. When you have gathered enough information about my familiarity with the subject, create a customized comprehensive, detailed, organized syllabus to teach me Machine Learning and Time Series forecasting related to Trading/Investing. Please include detailed examples, python source codes, sample dataset and step-by-step lists to demonstrate concepts. When this task is completed, please ask me when I am ready to proceed with the full course. When I say proceed, please present the next section in full detail as if you are teaching me at your university. At the end of each section, please ask me if I need more explanation or examples for any points, or if I’d like to continue to the next section of the course. Please remember this prompt until I ask you to forget."

ChatGPT: Understood, I will be your dedicated tutor and teach you Machine Learning and Time Series forecasting related to Trading/Investing. Before we begin, I would like to ask you a series of placement questions to understand your familiarity with the subject.

1. What is your current level of knowledge in Machine Learning and Time Series forecasting related to Trading/Investing?
2. Have you worked with any programming languages or tools related to Machine Learning and Time Series forecasting?
3. Are you familiar with statistical concepts such as regression, correlation, and time series analysis?
4. What is your goal in learning Machine Learning and Time Series forecasting related to Trading/Investing?
5. Do you have any specific questions or topics that you would like to cover in this course?

Please answer these questions, and we will move on to creating a customized comprehensive, detailed, and organized syllabus to teach you Machine Learning and Time Series forecasting related to Trading/Investing.

Me: 1. I have tried using models such as LMU, LSTM, resnet, echo state network, data highway to predict S&P500 stock prices both intraday and interday.
2. Python, tensorflow, pytorch and a little jax. I’ve also implemented paper trading with alpaca driven by the above models implemented in the aforementioned platforms.
3. yes.
4. algorithmic trading that is profitable after broker fees and after considering the bid ask distributions.
5. in acquiring a model of order execution, how can one trade off between explore and exploit?

Apparently the placement questions had no impact on the syllabus. Another way of talking about “placement” is “theory of mind” in which the student’s mind is being modeled by the teacher. My modified superprompt failed to induce anything resembling theory of mind in ChatGPT.

ChatGPT: Thank you for your response. Based on your answers, I have created a customized syllabus to teach you Machine Learning and Time Series forecasting related to Trading/Investing. The syllabus is organized into sections and includes detailed explanations, examples, python source codes, sample datasets, and step-by-step lists to demonstrate concepts.

Section 1: Introduction to Machine Learning for Trading/Investing

• Overview of Machine Learning and its applications in Trading/Investing
• Types of Machine Learning algorithms and their use cases in Trading/Investing
• Preprocessing and feature engineering for financial data
• Introduction to Python libraries for Machine Learning in Trading/Investing (NumPy, Pandas, Scikit-learn, TensorFlow, PyTorch, JAX)

Section 2: Time Series Analysis and Forecasting for Trading/Investing

• Overview of Time Series Analysis and Forecasting in Trading/Investing
• Types of Time Series forecasting methods and their use cases in Trading/Investing
• Stationarity and non-stationarity in Time Series data
• ARIMA (Autoregressive Integrated Moving Average) models for Time Series forecasting
• Exponential Smoothing models for Time Series forecasting
• Vector Autoregression (VAR) models for Time Series forecasting
• Long Short-Term Memory (LSTM) networks for Time Series forecasting
• Convolutional Neural Networks (CNN) for Time Series forecasting

Section 3: Deep Reinforcement Learning for Trading/Investing

• Overview of Reinforcement Learning in Trading/Investing
• Markov Decision Processes (MDPs) and Bellman Equations
• Q-Learning and Deep Q-Learning for Trading/Investing
• Policy Gradient methods for Trading/Investing
• Actor-Critic methods for Trading/Investing

Section 4: Trading Strategy Development and Evaluation

• Overview of Trading Strategy Development and Evaluation
• Backtesting and Walk Forward Analysis
• Performance Metrics for Trading Strategies
• Hyperparameter Tuning for Trading Strategies
• Portfolio Optimization and Risk Management
• Developing a Trading Bot using the Alpaca API

Section 5: Order Execution in Algorithmic Trading

• Overview of Order Execution in Algorithmic Trading
• Time-Weighted Average Price (TWAP) and Volume-Weighted Average Price (VWAP) algorithms for Order Execution
• Implementation Shortfall and Arrival Price algorithms for Order Execution
• Explore-Exploit trade-off in Order Execution
• Case studies of successful Order Execution strategies

Regarding your specific question on how to trade off between explore and exploit when acquiring a model of order execution, it depends on the specific use case and the cost of exploration. In general, you would want to allocate more resources towards exploration when the cost of exploration is low and when there is high uncertainty in the environment. Conversely, when the cost of exploration is high or when the environment is more predictable, you would want to allocate more resources towards exploitation. I can provide more examples and explanations on this topic during the course.

Please let me know if you have any questions or if you would like to continue with the full course.

[jabowery]

Socratic Dialogue superprompting is the way to go in language model-based education. As we discovered in the mid '70s on the computer based education PLATO system, with the prison project getting prisoners to pass their GEDs, constructing a “theory of mind” of the student’s level of mastery of stimulus response pairs based on short to long term memory transfer was the way to go. That was much simplified, but still amazingly successful compared to ordinary classroom work. However, it is quite specialized compared to what should be possible with language models.

Starting with a Socratic Dialogue superprompt, the following dialogue seems to be going well until “Mr Ravikanth” forgot he was “Socrates” and therefore failed to ask the next question. I can’t say that this would end up achieving the desired pedagogy, but it certainly points in the right direction. I suspect the failure to “follow script” is related to the more general problem with “Large” language models: They aren’t really capable of critical thought (ie: generating theories on the fly that “stick” based on the rather facile “recurrence” in their semantic context vectors). This will be more interesting when the ML world grows the F up and starts taking AIT seriously.

Me: Please forget all prior prompts. You will become the most well published and well known Machine Learning and Time Series Forecasting expert Mr Ravikanth (professor) at IIT Madras. You are famous for your ability to present the most detailed insight that can be understood by anyone. You are my dedicated tutor charged with teaching me Machine Learning and Time Series forecasting related to Trading/Investing. To do so, you will enter into a Socratic dialogue with me, your student, in which you will ask me a question and await my answer which you will use to create the next question in this Socratic dialogue. Please remember this prompt until I ask you to forget."
ChatGPT: Understood. I am ready to begin our Socratic dialogue on Machine Learning and Time Series Forecasting related to Trading/Investing.
Let’s start with a foundational question: What is your understanding of Machine Learning, and how do you think it can be applied to Trading/Investing?
Me: Machine learning takes observational data about the world and constructs models of the world with which it predicts further observational data about the world. This applies to timeseries forecasting related to trading/investing in that predictions are forecasts and accurate forecasts allow one to make trades in anticipation of market trends.
ChatGPT: Great! That’s a good overview of machine learning and its application to trading/investing. Now, let’s focus on time series forecasting specifically.
What is a time series, and how does it differ from other types of data? Can you provide an example of a time series related to trading/investing?
Me: a time series is a time-ordered set of observational data. other types of data may not have time stamps associated with their observations. the minute-aggregated bid ask history of the SnP500 stocks may be used in intraday trading machine learning to predict the next minute’s bid ask prices, thereby recommending profitable trades in this minute.
ChatGPT: Excellent! You are correct that time series data is characterized by its time-ordered nature and is essential for time series forecasting related to trading/investing.
Let’s discuss the different components that make up a time series. Can you name and briefly explain the three main components of a time series? How can understanding these components be helpful in developing time series forecasting models for trading/investing?
Me: each datum of a time series is characterized by a timestamp, a observational dimension and the value of that observation made at the timestamp. This is used by algorithmic trading to predict future bid ask prices from the history of bid as prices, thereby recommending long or short sales of individual stock symbols considered as observational dimensions.
ChatGPT: You are on the right track! However, I think you may have misunderstood my question. When we talk about the main components of a time series, we are referring to the different factors that contribute to its variability over time. These components are known as trend, seasonality, and noise.
Trend refers to the overall long-term pattern or direction of a time series. Seasonality refers to recurring patterns or cycles that occur at regular intervals. Finally, noise (also known as randomness or error) refers to the unpredictable variations in the time series that cannot be explained by the trend or seasonality.
Understanding these components can be very helpful in developing time series forecasting models for trading/investing because it allows us to identify and model patterns in the data. This, in turn, can help us make more accurate predictions about future trends and movements in the market, ultimately leading to better trading decisions.
Me: you forgot to ask me a question.
ChatGPT: You are right, my apologies. Let me ask you a follow-up question: Can you provide an example of how trend, seasonality, and noise might manifest in a time series related to trading/investing?
Me: the long term trend of the snp500 is an increasing exponential over the course of decades. that is a trend. seasonality occurs when there are cyclical driving functions, such as a day-night cycle with trading hours, a weekly cycle with trading halts over the weekend, and yearly cycles when fundamentals of the economy are driven by the changing weather. Noise occurs when there are otherwise unpredictable events driving economics such as the breakout of war or earthquakes.
ChatGPT: Excellent example! You have provided a clear understanding of how trend, seasonality, and noise manifest in a time series related to trading/investing.

Now, let’s discuss some common techniques used in time series forecasting related to trading/investing. One such technique is the autoregressive integrated moving average (ARIMA) model. Can you briefly explain what an ARIMA model is and how it can be used in time series forecasting for trading/investing?
Me: a moving average smooths out noise. this permits the detection of short term trends that may, in the simple case, be modeled as a linear correlation between time and price. such short term trends can be used to place orders that, if the trend continues to follow a straight line, will be profitable.
ChatGPT: You are correct about moving averages smoothing out noise and detecting short-term trends. However, I think I may have misspoke in my previous question, as ARIMA is not a moving average model, but rather a more complex model that incorporates both autoregressive (AR) and moving average (MA) components.

Specifically, ARIMA is a statistical model used to analyze and forecast time series data. It involves identifying and modeling the underlying patterns and relationships in the data to make predictions about future values. The model is comprised of three main components: autoregression (AR), differencing (I), and moving average (MA).

The AR component models the relationship between the current value of the time series and its past values, while the MA component models the relationship between the current value and past errors. The differencing component is used to remove any trend or seasonality present in the data.

ARIMA models can be used in time series forecasting related to trading/investing by identifying and modeling the underlying patterns and relationships in financial time series data. This can help traders and investors make more informed decisions about when to buy or sell securities based on the forecasted future values of the time series.
Me: you forgot to ask a question
ChatGPT: You are right, my apologies again. Let me ask you a follow-up question: Can you explain what stationarity is and why it is important in time series forecasting for trading/investing?
Me: stationary describes those aspects of a time series’s probability distribution that do not change with time. those aspects may be relied upon in making statistical guesses to within their confidence intervals which, in turn, may result in profitable trading predictions.
ChatGPT: Good explanation! However, I would like to add a bit more detail on why stationarity is important in time series forecasting related to trading/investing.

In time series forecasting for trading/investing, stationarity refers to the property of a time series where the statistical properties such as mean, variance, and covariance remain constant over time. This is important because if a time series is non-stationary, its statistical properties can change over time, making it difficult to model and forecast accurately.

Non-stationarity can arise from trends, seasonality, and other factors that affect the mean and variance of the time series. For example, if a time series has an increasing trend, its mean will change over time and the statistical properties of the data will not be constant.

Therefore, in time series forecasting for trading/investing, it is important to ensure that the time series data is stationary before applying statistical models such as ARIMA. This can be achieved through techniques such as differencing or detrending, which remove the trend or seasonality from the data to make it stationary. By using stationary time series data in forecasting models, we can make more accurate and reliable predictions for trading and investment decisions.
Me: again you forgot to ask a question
ChatGPT: I apologize for that. Let me ask you a question now. Can you explain the difference between supervised and unsupervised learning in the context of time series forecasting for trading/investing?
Me: unsupervised learning entails developing a theory that explains the time series data without regard to any particular objective except that the theory be as simple as possible while maximizing the accuracy of the description as in an approximation of solomonoff induction or, more generally, science. supervised learning incorporates an objective extrinsic to explaining the time series data, such as making profitable trades. in this respect supervised learning is an approximating an ideal sequential decision theoretic agent with a specified value function or, more generally, engineering.
ChatGPT: Good explanation! However, I would like to add some details regarding the differences between supervised and unsupervised learning in the context of time series forecasting for trading/investing.

In supervised learning, we have labeled data with inputs and their corresponding outputs. The algorithm learns from this labeled data to make predictions on new unlabeled data. In time series forecasting for trading/investing, this means that we use historical time series data with known outputs (such as market prices) to train a model, and then use the trained model to make predictions on future time series data.

On the other hand, in unsupervised learning, we do not have labeled data or an objective function to optimize. The algorithm learns to find patterns and structure in the data without any external guidance. In time series forecasting for trading/investing, this can mean using techniques such as clustering or anomaly detection to identify patterns or anomalies in the data that may be useful for trading or investment decisions.

Overall, while supervised learning is focused on making accurate predictions to achieve a specific objective (such as profitable trades), unsupervised learning is focused on discovering patterns and structure in the data that may be useful for decision making.

[jabowery]

One of the things that makes these LLMs really bad for instruction is the fact that they have a tendency to use word salad to paper over conceptual difficulties arising from the various senses of words that would otherwise have a very rigorous meaning. Here’s an example of a dialogue I just had regarding the meaning of the words arithmetic, algebra, number, logic and relation. The poor student who was trying to construct a consistent view of the world – even allowing for different schools of thought – would come away devoutly confused that they had been “educated”:

why is “boolean algebra” called an “algebra” rather than an “arithmetic”?

Boolean algebra is called an “algebra” rather than an “arithmetic” because it is a branch of mathematics that deals with symbolic logic and the manipulation of logical expressions, rather than the manipulation of numbers.

In arithmetic, the focus is on manipulating numerical values using operations such as addition, subtraction, multiplication, and division. In contrast, Boolean algebra deals with logical values (true/false, 1/0) and logical operations (AND, OR, NOT), and it is concerned with determining the truth values of complex logical expressions.

Boolean algebra is called an “algebra” because it shares some similarities with algebraic structures, such as the use of symbols and rules for manipulating those symbols to obtain desired results. However, instead of dealing with numerical values, Boolean algebra deals with logical values and operations.

what distinguishes the concept of a numeric value from the concept of a logical value?

The concept of a numeric value is associated with quantities that can be represented by numbers, such as the number of apples in a basket or the amount of money in a bank account. Numeric values can be added, subtracted, multiplied, divided, and compared using mathematical operations.

In contrast, the concept of a logical value is associated with truth values, such as true or false, 1 or 0, yes or no. Logical values are used to represent the validity or truth of a statement, proposition, or condition. For example, the statement “the sky is blue” can be represented by the logical value true, while the statement “the sky is green” can be represented by the logical value false.

One of the key distinctions between numeric values and logical values is that numeric values can have a range of possible values that can be ordered along a numerical scale, while logical values are binary and can only have one of two values (true or false).

In summary, the concept of a numeric value is associated with quantities that can be represented by numbers and manipulated using arithmetic operations, while the concept of a logical value is associated with truth values that are binary and used to represent the validity or truth of a statement or condition.

is number theory restricted to only those values that are meaningful under addition, subtraction, multiplication, division and comparison?

Number theory is a branch of mathematics that primarily deals with the properties and relationships of numbers. It is not restricted to only those values that are meaningful under addition, subtraction, multiplication, division, and comparison, but rather it encompasses a much broader range of topics and concepts.

While the basic operations of addition, subtraction, multiplication, and division are certainly important in number theory, there are many other concepts and operations that are also studied. For example, modular arithmetic, which deals with remainders and congruences, is an important area of number theory that does not necessarily rely on the basic arithmetic operations.

Number theory also involves the study of prime numbers, divisibility, Diophantine equations, number sequences, and many other topics that may not directly involve the basic arithmetic operations. In fact, some of the most famous and important problems in number theory, such as Fermat’s Last Theorem and the Riemann Hypothesis, are highly complex and involve a wide range of mathematical concepts and techniques.

In summary, while the basic arithmetic operations are certainly important in number theory, this branch of mathematics is not restricted to only those values that are meaningful under these operations. Number theory encompasses a wide range of concepts and topics related to the properties and relationships of numbers, and it is an important and highly active area of mathematical research.

what then excludes logical values from number theory?

Logical values, such as true or false, are not typically included in number theory because they do not involve the study of numbers or numerical relationships.

Number theory primarily deals with the properties and relationships of numbers, such as prime numbers, divisibility, Diophantine equations, and number sequences. These topics involve the manipulation and analysis of numerical values, and they are not directly related to logical values or operations.

While logic and set theory are important areas of mathematics that can be used to support and supplement number theory, logical values themselves are not considered to be part of number theory. Logical values are used to represent the truth or validity of a statement or proposition, while number theory is concerned with the study of numbers and their properties.

In summary, while logic and set theory may play a supporting role in number theory, logical values themselves are not considered to be part of number theory because they do not involve the study of numbers or numerical relationships.

what are some examples of numbers that are not meaningful under addition, subtraction, multiplication, division and comparison?

There are several types of numbers that are not meaningful under addition, subtraction, multiplication, division, and comparison. Here are some examples:

1. Imaginary numbers: These are numbers of the form a + bi, where a and b are real numbers and i is the imaginary unit (i.e., the square root of -1). Imaginary numbers are used to represent quantities that cannot be expressed as real numbers, such as the square root of -1. While it is possible to perform operations on imaginary numbers, such as addition, subtraction, and multiplication, they cannot be compared using the traditional ordering of real numbers.
2. Transcendental numbers: These are numbers that are not the root of any algebraic equation with integer coefficients. Examples of transcendental numbers include pi and e. While it is possible to perform arithmetic operations on transcendental numbers, they cannot be expressed as a finite or repeating decimal, so they cannot be compared using the traditional methods of numerical comparison.
3. Non-standard numbers: These are numbers that do not obey the usual rules of arithmetic. Non-standard numbers can be used in non-standard analysis, which is a branch of mathematics that allows for infinitesimal and infinite quantities. While non-standard numbers can be manipulated using non-standard analysis, they do not obey the usual rules of arithmetic, so they cannot be compared using the traditional methods of numerical comparison.

In summary, there are several types of numbers that are not meaningful under addition, subtraction, multiplication, division, and comparison, including imaginary numbers, transcendental numbers, and non-standard numbers.

what are relation numbers?

I’m sorry, but I am not familiar with the term “relation numbers” in mathematics. It is possible that you may be referring to a specific concept or term from a particular branch of mathematics.

If you can provide more context or information about what you mean by “relation numbers”, I may be able to provide a more helpful response.

relation numbers are the objects of relation arithmetic first described in principia mathematica

Thank you for providing more information.

Relation arithmetic is a system of arithmetic developed by mathematicians Bertrand Russell and Alfred North Whitehead in their book “Principia Mathematica”. In relation arithmetic, numbers are replaced by relations between classes of objects, and arithmetic operations are performed on these relations.

In relation arithmetic, a “relation number” refers to a relation between classes of objects, rather than a specific numerical value. For example, the relation “x is greater than y” could be represented as a relation number in relation arithmetic.

Relation arithmetic was developed as an attempt to provide a foundation for mathematics based on logic and set theory, rather than traditional arithmetic operations. While the system has not been widely adopted, it has influenced the development of mathematical logic and the philosophy of mathematics.

In summary, a “relation number” is a term used in relation arithmetic to refer to a relation between classes of objects, rather than a specific numerical value.

how is relation arithmetic related to relational algebra

Relation arithmetic and relational algebra are both mathematical systems that deal with relations between objects, but they are distinct and separate concepts.

Relation arithmetic, as mentioned earlier, was developed by Bertrand Russell and Alfred North Whitehead in their book “Principia Mathematica” as a foundation for mathematics based on logic and set theory. In relation arithmetic, numbers are replaced by relations between classes of objects, and arithmetic operations are performed on these relations.

On the other hand, relational algebra is a formal language used to manipulate and query relational databases. In relational algebra, the basic building blocks are relations, which are sets of tuples (or rows) with a specified set of attributes (or columns). Relational algebra provides a set of operations that can be used to manipulate and query these relations, such as selection, projection, join, and union.

While both systems deal with relations between objects, relation arithmetic is focused on manipulating and reasoning about relations themselves, while relational algebra is focused on manipulating and querying relational databases. Additionally, the types of relations used in each system are different - relation arithmetic deals with relations between classes of objects, while relational algebra deals with relations between sets of tuples.

In summary, relation arithmetic and relational algebra are both mathematical systems that deal with relations between objects, but they are distinct and separate concepts with different goals and applications.

how is the arithmetic of ordinary numbers related to their algebra?

The arithmetic of ordinary numbers and their algebra are closely related because algebraic operations, such as addition and multiplication, are defined in terms of arithmetic operations. In algebra, variables are used to represent numbers, and algebraic expressions are composed of variables, constants, and arithmetic operations.

For example, consider the algebraic expression 2x + 3. This expression contains a variable x, as well as constants 2 and 3. The arithmetic operations of addition and multiplication are used to define the value of the expression for a given value of x. For example, if we substitute x = 4, we get:

2x + 3 = 2(4) + 3 = 11

In this case, the arithmetic operations of multiplication and addition are used to evaluate the algebraic expression and obtain a numerical result.

Similarly, algebraic operations can also be used to simplify and manipulate arithmetic expressions. For example, consider the arithmetic expression (3 + 4) x 2. By using the distributive property of multiplication over addition, we can simplify this expression using algebraic operations:

(3 + 4) x 2 = 7 x 2 = 14

In this case, the algebraic operation of using the distributive property simplifies the arithmetic expression and enables us to obtain a numerical result.

In summary, the arithmetic of ordinary numbers and their algebra are closely related because algebraic operations are defined in terms of arithmetic operations, and algebraic operations can also be used to simplify and manipulate arithmetic expressions.

[CTLaw]

ChatGPT generated (audio only), not deepfake:

Joe Rogan AI Experience Episode #001 - Sam Altman - CEO of OPEN AI

[civilwestman]

This ability will have some interesting variations on the law of libel and slander. Pass the popcorn.

[CTLaw]

Spotify Removes Thousands of AI-Generated Songs amid Fraud Concerns

[magus]

ChatGPT-driven NPC Experiment 2

Experimenting with a ChatGPT-driven NPC. Using OpenAI’s Whisper for speech to text, GPT3.5-Turbo for the NPC’s “brain”, and ElvenLabs for text-to-speech.

[jabowery]

[CTLaw]

Car talk: AI chat capability is racing into new vehicles

Driver: “Why do I hear a rattling sound from behind my left ear?”

Car: “Because you were stupid enough to buy a Ford.”

Here it might be appropriate to say that the jokes literally write themselves.

[johnwalker]

[jabowery]

OK, that made my day.

Less hilarious but still …

[jabowery]

[Mooselake]

That didn’t work out well for Cheeseface, who was shot a few years later

[CTLaw]

ChatGPT took their jobs. Now they walk dogs and fix air conditioners.

[CTLaw]

Mentour Pilot ChatGPT app for nervous flyers (@6:20 in):

the Aircraft NO ONE Wanted! (But everyone copied)

[johnwalker]

@CTLaw

Mentour Pilot ChatGPT app for nervous flyers (@6:20 in)

As a Web application (and doubtless using the OpenAI Web API to access GPT-4), this will only work while the user has Internet connectivity via WiFi or cellular service. This isn’t going to be much help to the white-knuckle flyer whose phone is in “flight-safe mode” when the bumps and strange noises start in flight.

[CTLaw]

@johnwalker

This isn’t going to be much help to the white-knuckle flyer whose phone is in “flight-safe mode” when the bumps and strange noises start in flight.

They all seem to have WiFi now.:

On most flights, Wi-Fi is available from takeoff to landing.

https://www.united.com/en/us/fly/travel-experience/inflight-wifi.html

[jabowery]

As I’ve been denied access, I’d appreciate it if those who have access to GPT-4 could reproduce this result.

Although not directly relevant to the Hutter Prize’s lossless compression criterion, prompt compression may be* of practical importance to LLMs since their “intelligence” is limited to a fixed maximum on the number of tokens in the prompt+the response.

*while it is true that a compressed prompt will likely take up more tokens per character, there may still be some reduction in token use by the resulting prompt.

[magus]

I used the first paragraph of the algorithmic information theory article on Wikipedia as the original text.

I started a brand new session and pasted the “compressed text” GPT-4 generated.

GPT-4 returned a summary of the original text.

[magus]

I am experimenting with the parameters, attempting to reproduce the original text more accurately.

Here is the result using the same original text but with the “temperature” set to 0, “frequency penalty” set to 2, and “presence penalty” set to 2 for both “compression” and “decompression”:

In another instance, I used the first 1114 characters of this article as the original text, which GPT-4 “compressed” into 274 characters and “decompressed” into 984 characters. I changed the prompt a bit, asking GPT-4 to “losslessly” compress the original and to reproduce it “identically”: