In a paper posted on arXiv on 2023-03-20, “An aperiodic monotile”, four authors report discovery of a polygonal shape that tiles the plane but never repeats in arbitrarily large patches. This is called an “aperiodic tiling”, the best example of which is those discovered in 1973 and 1975 by Roger Penrose, the Penrose tiling, which requires only two polygons.
But is there a single tile which tiles the plane aperiodically? Yes, there is, say the authors of this paper and, in fact, there is a continuum of such tiles. Here is the abstract.
A longstanding open problem asks for an aperiodic monotile, also known as an “einstein”: a shape that admits tilings of the plane, but never periodic tilings. We answer this problem for topological disk tiles by exhibiting a continuum of combinatorially equivalent aperiodic polygons. We first show that a representative example, the “hat” polykite, can form clusters called “metatiles”, for which substitution rules can be defined. Because the metatiles admit tilings of the plane, so too does the hat. We then prove that generic members of our continuum of polygons are aperiodic, through a new kind of geometric incommensurability argument. Separately, we give a combinatorial, computer-assisted proof that the hat must form hierarchical – and hence aperiodic – tilings.
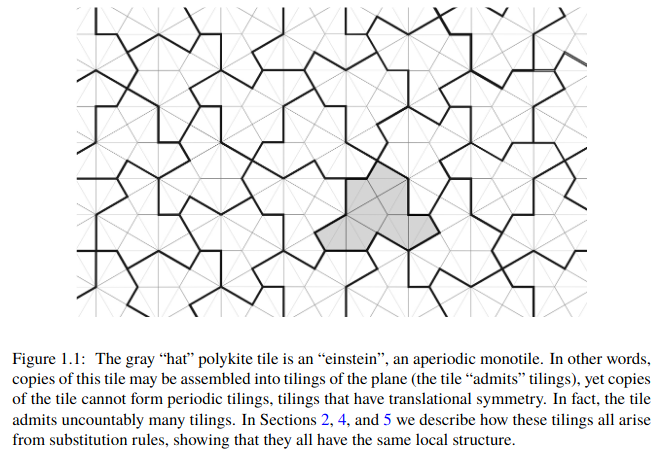
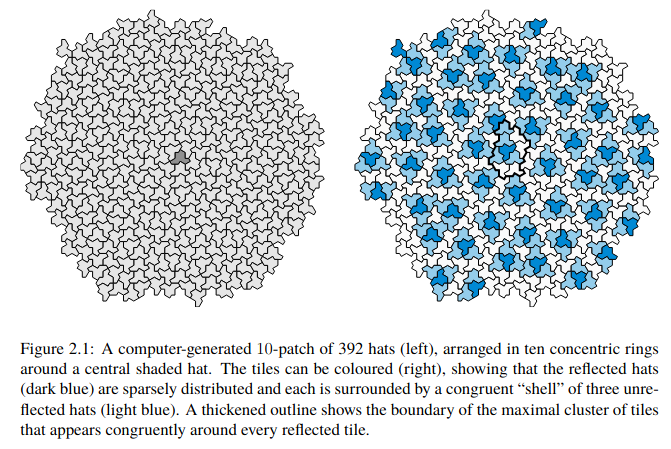

The entire paper is 89 pages in length, including proofs that the shape tiles the plane and is aperiodic.
Thanks to Rudy Rucker for discovering this paper.