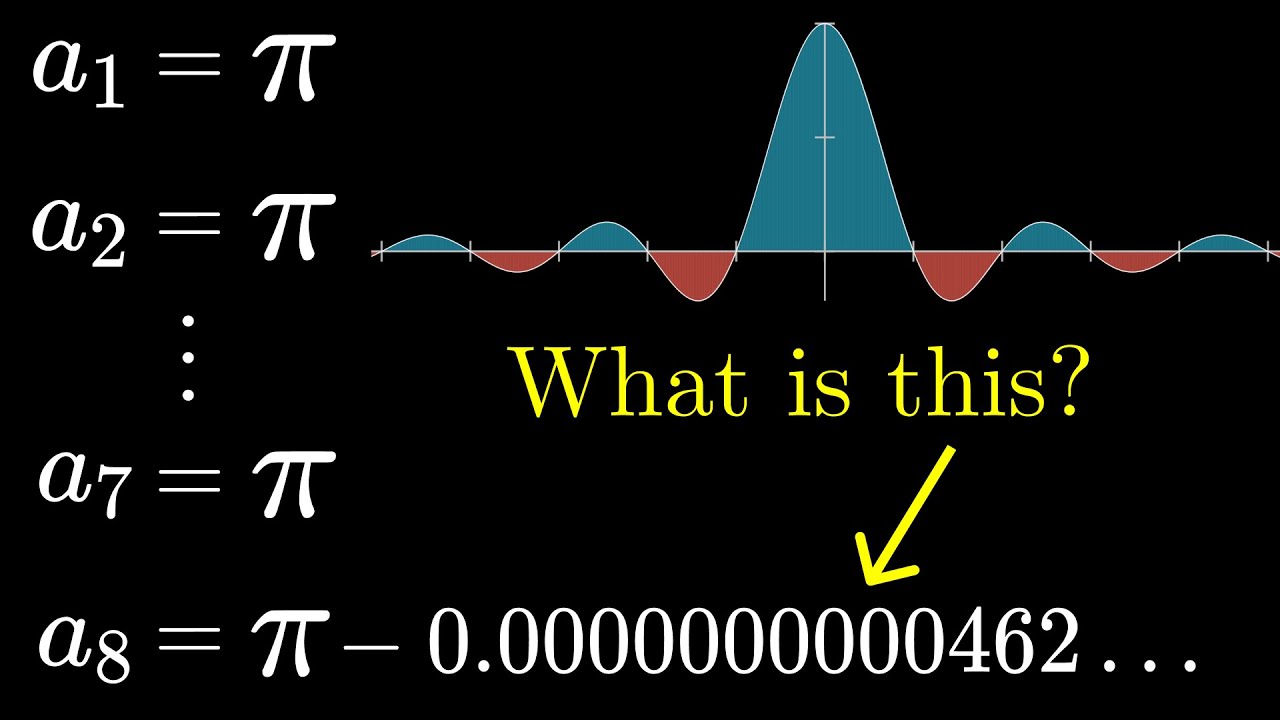
Here is more on Borwein integrals and John Carlos Baez on “Patterns that Eventually Fail”.
tilt
Love it. This is pretty good example of why Popper’s falsification dogma is dogshit and people should have been using algorithmic information (Turing complete lossless compression) of observations for model selection since at least the mid 1960s. “Falsification” as model deselection criterion tosses the recursively expanded integral into the same dustbin of history, upon reaching denominator=15, that welcomed phlogiston a century earlier. But that ignores how well the algorithmic hypothesis fit the pattern of observations and how little it departed from observation at the point of “falsification”. Such qualitative thinking is a quite literally and absolutely insane “philosophy of science” that has done vast amounts of damage to public discourse in the age of algorithmic predictions – most severely in the soft sciences that have the greatest impact on public policy.
The tiny amount of error that appears requires very little in the way of bits to encode as a literal correction to the algorithm – so little, in fact, that the algorithm almost certainly continues to be competitive as the preferred model in the face of the kinds of hypotheses likely to be churned out by “studies” majors writing for Huff Post. Moreover, to serious scientists, the tiny error is not discarded (lossless – remember?) although it might be ignored for practical purposes except by the eye trained in Fourier analysis. That eye sees a pattern not in the data qua data but a pattern in the information as algorithm. When the error appears that eye invests the brain cycles to look at related algorithms such as convolution rather than just writing it off as “measurement error”.
The Huff Post “studies” majors would, in that counterfactual world, have thrown their “hypotheses” against the model selection criterion of algorithm length – including errors as literal codes – and been rejected automatically by the simple expedient of doing a numeric comparison of lengths after the proffered algorithm ran. The serious scientists didn’t even spend a neuron cycle arguing with them, let alone worry about losing tenure because they didn’t pay close attention to the “studies” major.
The key to getting this part of data driven science right is to recognize that one is never dealing with an isolated dataset in a closed system – but with Reality in which fields of science are interrelated and that therefore the investment in a more complex algorithm that fits the data perfectly might well amortize its loss (bits) in more parsimonious explanations elsewhere. Big Data keeps us from being autistic so long as it provides a wide variety of perspectives on Reality.
Thank you, Mr. W., for drawing our attention to these excellent math videos. The power of explanation using modern graphical techniques is so much stronger than the old-fashioned way so many of us stumbled through earlier in life.
Another feature of this excellent video is the reminder that mathematics is basically a rather creative discipline. Multiply top & bottom by pi? Why not? Let’s try it and see!
Now on to convolution … which some have seen as the mathematical equivalent of crossing the Rubicon. ![]()