“Wait! Water is incompressible, right?”
Well, to be exact, water isn’t very compressible, but squeeze it hard enough and it will yield. The compressibility of water at 0° C is 5.1\times 10^{-10}~{\rm Pa}^{-1}, so at 4 km in the deep ocean (a little deeper than the wreck of the Titanic at 3800 metres), water is compressed around 2% by volume. At the bottom of the Mariana Trench at around 20 km, the water, under a pressure of 1000 bars (times standard atmospheric pressure) is about 5% denser than at the surface.
But why stop there? With a 150 tonne hydraulic press driving a piston to amplify the force, it’s possible to achieve a pressure of 2000 bars, twice that of the deepest point in the oceans. Units Calculator computes compression under such pressure as:
(5.1e-10/pascal) * (2000 bar) = 10.2 percent
What will happen to ordinary objects under such pressure? Scuba tanks are typically pressurised to between 200 and 300 bars, so it would be amusing see if one, fully filled with air, was crushed by this pressure, but sadly the test cell is insufficiently large. I haven’t been able to find the pressure specification for those 8 gram carbon dioxide cartridges used in soda siphons: it would be interesting to subject one to 2000 bars.
7 Likes
This leads me to wonder if sufficient pressure can cause water to crystallize - i.e. form ice. At the same time, I am guessing that compressing water is likely to raise the temperature. I really don’t know how to approach these questions, as I understand that neither Boyle’s nor Charles’ laws apply to liquids.
2 Likes
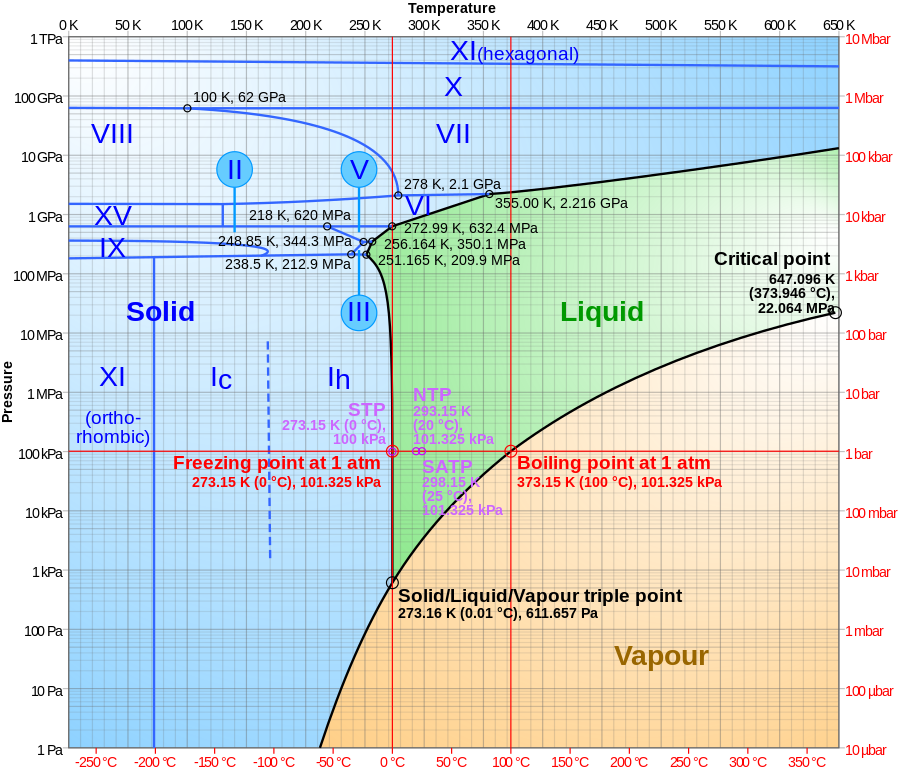
The behaviour of water under temperature and pressure is described by its phase diagram, as given below (click to enlarge).
The pressure scale in bar (units of average atmospheric pressure) is given on the right and pascals (newton per square metre) on the left and temperature at the top (Kelvin) and bottom (Celsius). Water is liquid only in the green part of the phase diagram. Above around 150,000 bar, water assumes a crystalline form even at temperatures as high as 600° K (approaching twice its boiling point at atmospheric pressure). For water at “room temperature” (around 25° C, 298° K), water solidifies around a pressure of 10,000 bar. The pressure in this experiment was one fifth that, 2000 bar.
Note that the ice which will form under such compression is not the regular ice from freezing at atmospheric pressure, but one of the other phases of ice such as Ice VI or Ice VII, of which 19 are known so far. Regular ice has a hexagonal crystal structure. Ice VI is tetragonal, while Ice VII is cubic.
Compressing will raise the temperature, but if there is a heat sink to conduct away the heat energy, the temperature will remain constant. For example, water under compression deep in the ocean is not at an elevated temperature because water is a good conductor of heat and conduction and convection will carry away the heat of compression.
5 Likes
I wonder what the phase transition energies are between solid forms?
(Ice IX: Shades of Cat’s Cradle!)
4 Likes