Cursed Units in Science and Engineering

[johnwalker]

Cursed Units

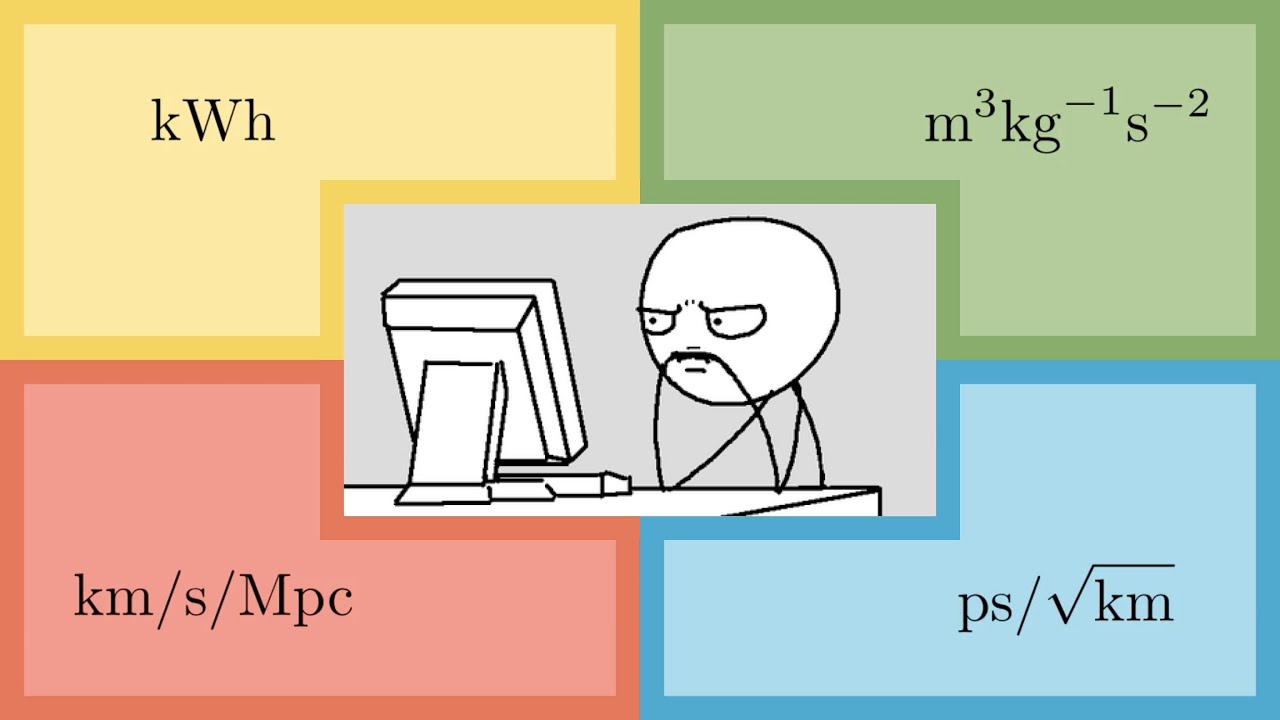
Not only must scientists and engineers contend with a plethora of legacy units used to measure various quantities (for example, “pint”, a unit of volume whose definition depends upon whether you are measuring a liquid or something dry and where and when you happen to be living). There are at least ten definitions of “pint”, varying from 250 (Flanders) to 1696 (old Scotland) millilitres), but some units in present-day use just make you say “What?” when you think about them.

Consider the way the Americans measure vehicle fuel economy: “miles per gallon”, where they’re trying to convey how many of their “miles” (as opposed to nautical miles, or Roman miles, or Italian miles, or Chinese miles, inter alia) a vehicle can travel on a gallon (U.S., not imperial) of gasoline (whatever that may be). But let’s write out that unit, then convert the components to SI units.

\frac{\rm mile}{\rm gallon}=\frac{1609.344\ {\rm metre}}{3.785\ {\rm litre}}

But metre is a unit of length, and litre is a unit of volume, which has dimension of length cubed, with:

{\rm litre}=0.001\ {\rm metre}^3

So we can simplify:

\frac{\rm mile}{\rm gallon}=\frac{1609.344\ {\rm metre}}{0.003785\ {\rm metre}^2}

This lets us cancel units and divide the numbers, yielding:

\frac{\rm mile}{\rm gallon}=\frac{425143.71}{\rm metre^2}

This is the “*What?” moment. They’re measuring fuel economy in units of reciprocal area? What the heck does that mean?

Well, actually, if you think about it, it does have a kind of perverse meaning. Let’s rescale from metres to milimetres to make the number on the right more tractable, yielding 0.42514371/{\rm mm}^2=0.42514371\ {\rm mm}^{-2}. If we take the reciprocal of the unit, we get:

\frac{\rm gallon}{\rm mile}=2.3521458\ {\rm mm}^{2}

This area, around 2.35 square millimetres, is the area of a tube of gasoline which the vehicle would have to consume as it drove along to replace the fuel it burned at the rate of one gallon per mile.

This is a particularly simple case of which you can, with a little mind-bending, make sense. But what about the unit astronomers and cosmologists use to express the expansion rate of the universe?

{\rm kilometre}/{\rm second}/{\rm megaparsec}

When you cancel out the units, this has dimensions of:

\frac{1}{\rm second}={\rm Hertz}={\rm Becquerel}

or frequency.

What?

[jabowery]

Its worse than you imagine (although perhaps not worse than you can imagine):

To quote the suicidal mathematical genius character, Alicia Western, in Stella Maris (Cormac McCarthy’s last novel):

But even Frege doesnt get completely down to nuts and bolts. Adding and subtracting are not really mathematics. A sack of pebbles will do. But multiplication and division are a different matter. If you were to multiply two tomatoes by two tomatoes you wouldnt get four tomatoes. You would get four tomatoes squared. So what is the two? Well. It’s an independent abstract mathematical operator. Oh? And what is that? We dont know. We made it up.

I turned down an opportunity to get in on the ground floor of Paypal because of what some would think of as the problem of “units” in programming languages but turned out to be about fixing a bug in Principia Mathematica.

I’d just put together the internet’s very first federated login system because HP’s divisions were all setting up their own customer relation management systems with independent login registrations. It was Hell but it worked well enough that BEA Systems took the idea and ran with it. So I was well positioned to catch the DotCon wave when HP announced their “Internet Chapter 2” project on which they were to blow something like a $500M. But I was even more motivated than that because (rewinding back to 1982) I’d been interfacing with David P. Reed (chief scientist at Lotus) and Xerox PARC on coming up with a network programming standard for AT&T’s mass market networking joint venture with Knight Ridder – and didn’t want to screw it up for obvious reasons. I’ve probably described that stuff elsewhere but it is no coincidence that I ended up at Software Arts’s suite at their introduction of TK!Solver – their units-based sequel to VisiCalc – at a conference in Houston that summer. I actually didn’t expect to see Reed (or my PLATO colleague Ray Ozzie) in their suite, but there we all were.

By 1999 I had identified the late Tom Etter as the guy I wanted to support with what precious little influence I had on the “Internet Chapter 2” project, because he had addressed two foundational issues in something he called “Link Theory”:

1. Parallelism implicit in relational semantics.
2. Temporal semantics grounded in imaginary logic “states” emergent from a theory of quantum computer programming.

I knew I wanted to incorporate units into this some how – especially since I’d recently done work with Roger Gregory on a rocket engine where I made extensive use of TK!Solver and Calchemy (which solves some under specified expressions by dimensional analysis) – but it wasn’t immediately obvious how to do this.

What Tom came up with was a number theory based on his Link Theory which fixed a bug in Principia Mathematica’s idea of Relation Arithmetic. Russell lamented that his notion of Relation Numbers never caught hold since it provided a way of relating to what he called “The Empirical World”. Relation Numbers are what people think of as numbers with empirical dimensions.

PS: I didn’t know until just a few months ago that Tom was an attendee of the 1956 Dartmouth AI Summer Workshop.

PPS: A “cursed unit” people sometimes run into is torque vs energy ending up with the “same” dimensions. I answered a physics stackexchange question regarding this:

Think in terms of coordinate transforms as a generalization of unit conversions.

When converting between units, you are doing a very simple coordinate transform on the, single, corresponding physical dimension:

Multiplication*.

When adding two angles, you are really dealing with, for example, a polar coordinate system. The underlying territory (physics) remains the same but the map changes when you try to add two angles together. The new map is still a two dimensional one with Cartesian grids, but it is a warp of the old map – like a Mercator Projection of Earth. All of the concerns about the dimensionality of expressions like “tan(angle)” are then hidden in the coordinate transforms which are, themselves, dealt with as a generalization of units conversions.

With polar coordinates there is, in addition, a new twist in that one of the dimensions is finite – it wraps around. That means the map is actually a cylinder of infinite length but finite circumference. Modulo arithmetic then becomes key to the notion of commensurability.

As for vector quantities like “height-meter” and “length-meter” – they involve vector operations. Dimensional analysis can be applied to vector quantities and their operations just as it can be to scalar operations.

*Converting between temperatures is multiplication with an offset but it is still a coordinate transform on a single dimension.

PPPS: Here’s a video of the TK!Solver booth at the 1983 COMDEX:

Fall Comdex 1983 Part 1 of 3

[jdougan]

My personal favorite system of measurement:

a joke about measurement

[jabowery]

My recent work to refine the atoll replication approach led me into another dead-end attempt to solve a system of constraints using Mathematica’s physical dimensions and units. The “sage advice” offered? Use Mathematica to solve your problem without units and dimensions and then, once solved, go back in and adorn your calculation with units and dimensions. One of the “wise ones” even came in and chided someone using Mathematica’s “support” for units and dimensions for thinking that Mathematica was a programming language when it is actually a highfalutin mathematical system!

Too bad Steven Wolfram didn’t take the name “Mathematica” seriously enough to try to look at Principia Mathematica’s last volulme for relation arithmetic, quantity and measurement for a sound foundation. Tom Etter and I attempted to do that before India nuked the last hope for such a sound foundation – not just for programming but for mathematics itself. But India had better uses for the piddling money that was going our way: Hire coethnics who hadn’t a prayer of even asking the right question as I did, let alone providing a path to an answer as Tom Etter might have done.