“You might say the ‘hand of God’ wrote that number [137]” – Richard Feynman
You will notice that there is no mention of kabbalah =137 in Wikipedia.
The Times of Israel has this article that does talk about 137 = kabbalah:
https://blogs.timesofisrael.com/chayei-sarah-where-kabbalah-meets-physics/
At the risk of going completely mystical on ya’ll:
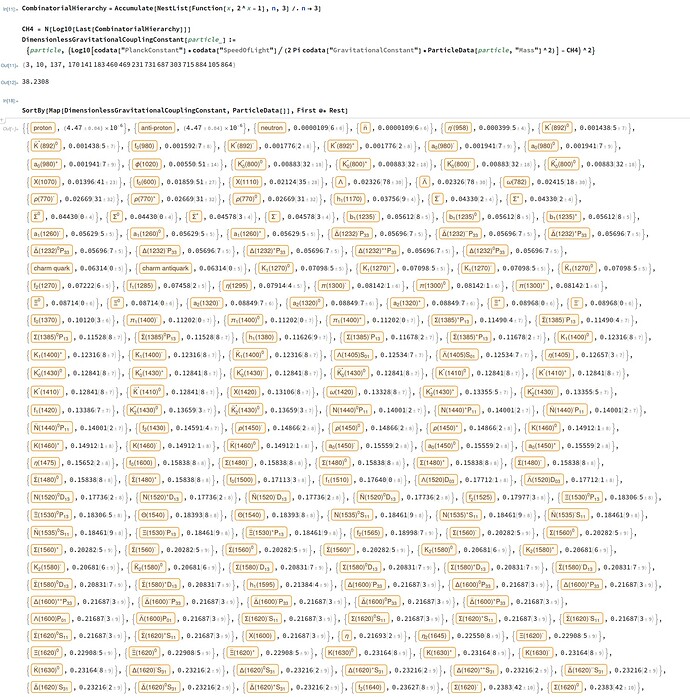
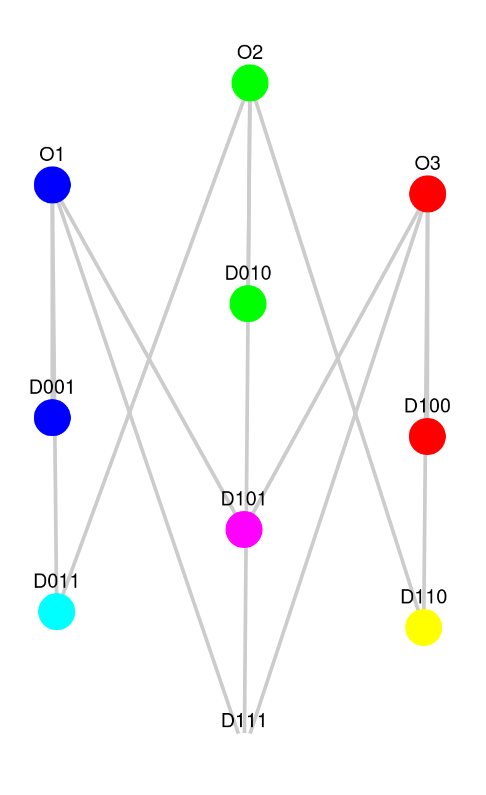
The Combinatorial Heirarchy’s first 3 numbers are:
3, 10, 137…
3 is, of course, all over the place in mystical traditions. But what’s this “10” business about? Well both Pythagorean and Kabbalah traditions place “10” at the center of their “esoteric” initiation. Pythagoreans required initiates to keep silent for years while contemplating the number 10 in the form of the Tetractys.
Kabbalah’s central model of the cosmos is the:
Sefirot (/sfɪˈroʊt, ˈsfɪroʊt/; Hebrew: סְפִירוֹת, romanized: Səfīrōt, Tiberian: Săp̄īrōṯ ),[1] meaning emanations , are the 10 attributes/emanations in Kabbalah,[2] through which Ein Sof (The Infinite) reveals itself and continuously creates both the physical realm and the chain of higher metaphysical realms (Seder hishtalshelus ).
I don’t know what Kabbalah’s cosmogony says about how 3 gives rise to 10, but…
Cosmogony concerns itself with the unfolding into primordial Creation and Perception of phenomena by primordial Being. As I understand Frederick Parker-Rhodes’s original motivation in formulating the Combinatorial Hierarchy, it was just such an approach to what might be called “The Inevitable Universe”:
The Inevitable Universe- Parker-Rhodes’ Peculiar Mixture of Ontology and Physics*
by H. PIERRE NOYES
Stanford Linear Accelerator Center Stanford University, Stanford, California 94309
THE SECOND PARKER-RHODES MEMORIAL LECTURE
Submitted to Proceedings of the 11 th Annual International Meeting of the ALTERNATIVE NATURAL PHILOSOPHY ASSOCIATION
Dept. of History and Philosophy of Science
Cambridge University Cambridge, England
September 14-l 7, 1989
- 2^2-1 = 3 (Trinity)
- 2^2-1 + 2^(2^2-1)-1 + 0 = 10 (Tetractys/Kabbalah Sefirot)
- 2^2-1 + 2^(2^2-1)-1 + 0 + 2^(2^(2^2-1)-1)-1 = 137 (Gematria of the Hebrew name for Kabbalah/ElectroMagnetism)
- 2^2-1 + 2^(2^2-1)-1 + 0 + 2^(2^(2^2-1)-1)-1 + 2^(2^(2^(2^2-1)-1)-1)-1 = 170141183460469231731687303715884105864 (Phenomenal Universe/Gravitation/Dirac Dimensionless Large Number Hypothesis)
The way we get from 3 to 10 in the Combinatorial Hierarchy is the recursive application of one layer of creation (the first being 3) to generate binary combinations which may be distinguished from that layer (ie: apply XOR) as well as from each other. In this case we have 3 entities/qualities/properties/attributes that may be present or absent in generating the 2^3-1 new, combination yielding 7 additional entities for a total of 10. This happens again with 2^7-1 to produce 137 in total, corresponding to the Electromagnetic scale. Then things go completely whacko and explode with 2^127-1 and we get gravitation. This may correspond to the kabbalah’s notion of the world coming into being in such an explosion that must be, in some sense, “repaired”.
What does kabbalah’s cosmogony say, if anything, about which 3 sefirot would be considered the progenators of the rest of the 10 sefirot?
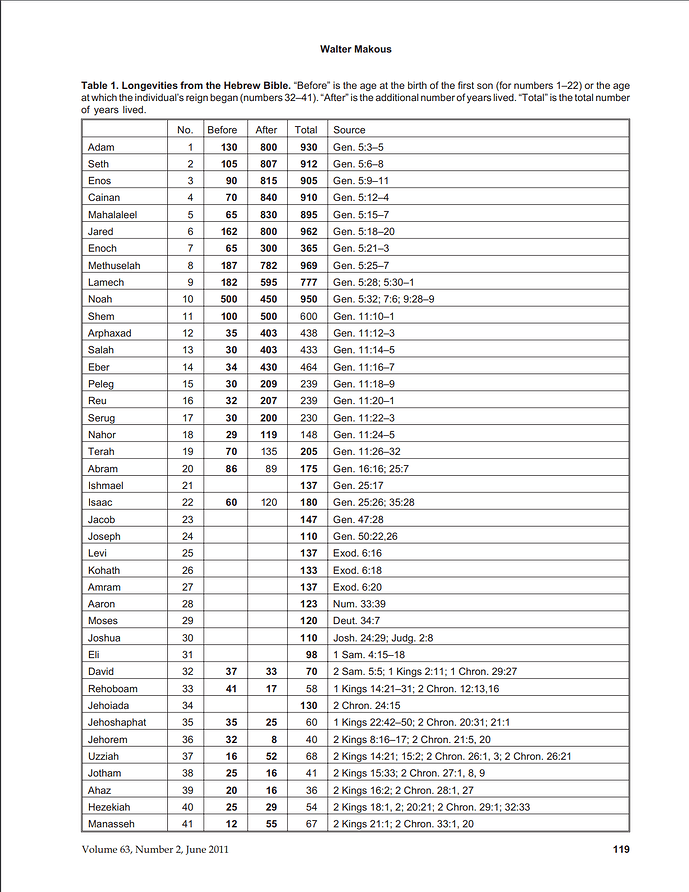
And we’re left with the “coincidental” Gematria of 137 for the Hebrew word for kabbalah which, at least in my mind, points to someone figuring out the Combinatorial Hierarchy who then influenced Gematria. But, if we are to believe the antiquity of the Old Testament’s references to 137 (Ishmael’s age at death, Levi’s age at death and Amram’s age at death (and, according to the Times of Israel article Abraham’s age when commanded to sacrifice Isaac – but I can’t find support for this)), it probably means that someone had figured it out at least that early, which would mean prior even to Pythagoras. In any event, this stuff seems encoded in the Old Testament, what ever the antiquity of those references.
PS: I have to testify to a rather “positive vibe” hitting me when studying this stuff of a quality I only rarely experience – like once a decade or two – in my life. This “positive vibe” last happened to me in 2000 one morning when I woke up and somewhat marveled at it since I had nothing to which I could attribute it. Then I checked hits on my website. The hits for the Bowery Award for Amateur Rocketry had gone through the roof – hundreds of times greater than ever. Wired magazine had published a story on the CATS prize that linked to it. Reflecting on the “magic” of this sort of thing is when we are dealing with the “ElectroMagnetics” of human society – particularly when we deal with mass media – there are potentials at work (perhaps Magnetic Vector Potentials). These potentials are a two-way street between the mind of God – as metacognitive source – and our own mind. These potentials may be put to “use” as “tools” to manipulate masses – bending them to our will – but where the positive vibes come from is their potential to reorient us toward God’s will. The phrase “moral compass” comes to mind – although I’ve seen that phrase used in ways that point to the stampede of the mob as the alignment – rather than a higher agency.