Battles over notation are some of the best (and most acrimonious) of battles!
7 Likes
What I find so disturbing about Heavisideâs âmurderousâ dislike of potentials is that the electric and magnetic fields both derive from the magnetic vector potential âAâ:
E=âA/ât (partial time derivative)
B=âxA (curl)
If you have the wave equation for A, you automatically have both. In fact, this is how I learned electromagnetism and it is also how Carver Mead proposes physics should be taught so as to incorporate modern understanding of what he calls âcollective electrodynamicsâ.
3 Likes
A more concise and complete form for electromagnetism in terms of potentials appears as a subexpression of the Lorentz force:
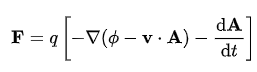
If you strip off the charge, you get an expression for a âmotionalâ E or motional electric vector field which depends on a velocity vector field v. The expansion of the total derivative of A with respect to time (dA/dt) contains the subexpression vxâxA, which is the magnetic portion of the Lorentz field.
It is really quite a puzzle to me that people donât work with this definition since it contains all the components necessary to calculate everything you need for EM.
1 Like
I donât know how many people around Scanalyzer follow Cormac McCarthy novels, but his most recent is inspired by the metaphysics of QM and contains this rather curious (to me) technical flaw:
Profound equations are often said to be beautiful Maxwell I suppose. If you overlook the E and B vector potential in place of the A.
This is echos, almost exactly, my prior comment except that the proper wording would have been âE and B fields in place of the A vector potentialâ.
This error confuses what may be a portal into the metaphysics he addresses since in my impression of the boundary between the paranormal and physics, it is the A vector potential that looms the largest.
3 Likes
âA History of Vector Analysis: The Evolution of the Idea of a Vectorial Systemâ, by Michael J. Crowe, originally published in 1967. Dover edition published 1994, ISBN 0-486-67910-1, 270 pages.
Kathy, who loves physics, strongly recommended this book. Ah! For those happy days half a century ago when authors could write and editors could edit. Kathy is right â this is a well-written interesting book, definitely worth reading.
Vectors are mathematical entities with both magnitude & direction. Vectorial analysis can be traced back to the late 1700s when Gauss began to play around with representing complex numbers on a plane. The pace picked up around 1843 when Sir William Hamilton invented quaternions. Eh? What on Earth is a quaternion? For that, we have to jump forwards about half a century to the view of that acerbic self-taught genius Oliver Heaviside: âA quaternion is neither a scalar, nor a vector, but sort of combination of both. It ⌠is a highly abstract mathematical conceptâ.
Hamilton himself was a certifiable genius who was appointed professor at Trinity College, Dublin while still an undergraduate. His justifiable fame resulted in his quaternions getting a reasonable amount of notice in mathematical circles. At almost the same time as Hamilton, Herr Grassmann, a humble German schoolmaster, independently created a vectorial system. However, academic outsider Grassmann was almost totally ignored.
Things really began to heat up in 1873 when the great James Clerk Maxwell published his theory of electricity & magnetism which was based on the use of âfieldsâ to explain action at a distance. Now, action at a distance is one of those concepts which becomes discomforting if one thinks about it too closely â but Maxwellâs theory was based on fields, which required him to make some use of the mathematics of Hamiltonâs quaternions.
Nearly two decades later Heaviside entered the fray and poo-pooed quaternions. He stripped Maxwellâs equations down to a modern vectorial form. Meanwhile, Willard Gibbs at Harvard â who is more commonly remembered these days for his work on thermodynamics â independently and simultaneously also generated the modern form of vectorial analysis.
Over the period 1890 â 1894, a mathematical bun fight broke out between the supporters of quaternions and those who preferred the emerging Heaviside-Gibbs formulation. Much ink was spilled on such topics as the peculiarity that the square of a quaternion had to be a negative number.
By 1910, physicists had concluded that the Heaviside-Gibbs vector formulation was more useful for dealing with real physical issues such as optics and electricity & magnetism. Academic debates over whether vectors should be represented by Gothic letters or Greek letters were resolved, and the modern system of vectorial analysis emerged. Herr Grassmannâs prescient contributions were still largely ignored. As the author notes: âGrassmann was unknown however and suffered the fate of a man whose first great discovery is revolutionaryâ.
The reader will not learn much about vectors from this book, but will enjoy a lot of fascinating history about the development of mathematics and physics.
5 Likes
When quaternions were originally developed, many mathematicians thought them extremely strange because, unlike real and complex numbers, multiplication and division of quaternions is not commutative. If \bf a and \bf b are arbitrary quaternions, except for a few special cases in which they reduce to less general number systems:
{\bf a} \times {\bf b} \neq {\bf b} \times {\bf a}
It was realised that quaternions were equivalent to rotation in three-dimensional space, with multiplication equivalent to first performing one rotation, then another. These operations do not commute either, and in fact behave precisely as quaternions do. (Think about it: if you have a cube and rotate it first around its X axis by 90° and then around its Y axis by 90 degrees, it will end up in a different orientation than if you first rotate in Y and then X. (Until you become comfortable with 3D rotations, this stuff may make your head explode. The Fourmilab Orientation Cube can help you grasp whatâs going on: here is a video demonstration.)
With the development of vector analysis, quaternions were largely displaced in physics and engineering by vectors, and were considered an arcane topic in abstract mathematics. All of this changed in the latter half of the 20th century with the advent of three-dimensional computer graphics, robotics, and spacecraft control and navigation, where quaternions allowed one to easily do mathematics on 3D rotations without the Hellish mess of trigonometric functions and risk of degeneracies and singularities that lurk when doing it the âeasy wayâ.
Today, most extensible application programming languages such as Python, Rust, Perl, Mathematica, and even C++ have packages that implement quaternion arithmetic.
6 Likes
I first learned to use quarternions as practical tools more than twenty years ago, programming ABB industrial 6-axis robots.
4 Likes
Greetings,
Iâd very much like to discuss this topic with you further if you ever have the time. I just signed onto this platform specifically so that I could discuss this with someone.
Unfortunately, I am a layman who does ITâŚso Iâm not a well versed mathematician or physicist, so itâs hard for me to decipher the pure math behind these concepts.
However, I have spent years reading and studying such things regardless, in hopes of forming an elementary understanding and more importantly, a geometrical conceptualization of these things.
Are you familiar with the Aharonov-Bohm, and Maxwell Lodge effects? I would imagine that you are given your previous explanations of the Magnetic Vector Potential.
As the video describes, Heaviside basically condemned the Magnetic Vector Potential to the realm of mathematical contrivanceâŚremoving from it the physical reality. The Aharonov-Bohm effect shows that the Vector Potential alone (without the magnetic field) can change the quantum interference pattern of an electron beamâŚthe Maxwell-Lodge effect can induce a current within an adjacent coil (again, where no magnetic field is present) by varying the current in the primary, solenoidal coil.
Both of these effects seem to have proven the physical reality of some type of field represented by the Magnetic Vector PotentialâŚI have only spoken to one other scientist about this in depth and he felt that the field described by the Magnetic Vector Potential might best be thought of as the âVortex Fieldâ akin to Joseph Larmorâs conceptualization of a rotationally elastic, but incompressible aether.
I have other lines of thought in regards to this, such as how the âElectromagnetic Missile Effectâ (The hyperbolic acceleration of electrons, creating large, uniform charge density waves or gradients at the interfaces of antenna with free space are what extend the Fresnel near field region of an electromagnetic system) might play into methods of long range Magnetic Resonant Wireless power. Basically, using what is termed the Fresnel Near Field region as a âvirtual waveguidââŚI came to this idea with the help of the other scientist I spoke with.
Anyway, I was wondering if youâd be interested in discussing these things? I have source material for the effects Iâve mentioned if you need it.
6 Likes
Way outside my knowledge, but welcome anyway.
3 Likes
After being seriously involved in the empirical aspects of the MVP â mainly from 2014-2016 and since 1/2024 â youâre correct to point out the âtwo effectsâ which I would say are not so much âeffectsâ as they are views of the physical reality of the MVP. All of the Aharonov Bohm folks deny there are classical effects. If you want the best of the Aharonov Bohm, quantum-only folks, follow Herman Batelaan. Most of those invested in the classical effects, while not in denial of the AB effect, are at best only mildly interested in quantum mechanics. Iâm in the latter camp, although Iâm more interested in the QM aspect than probably 99% of the folks who talk about stuff like âlongitudinal wavesâ or, even further out, conspiracy theories about Tesla, and vilify guys like Heaviside which I do not.
Now, before defending Heaviside â I admit that âlongitudinal wavesâ are âfringe physicsâ so let me now pretend that what our experiments demonstrated was, indeed, a classical effect that comports with âlongitudinal wavesâ. Iâm not a âtrue believerâ in âlongitudinal wavesâ â but Iâm sufficiently intrigued by what I saw in the scope traces and my efforts to mathematically model them to invest what few resources I have in refining those experiments.
The critical juncture was not Heaviside but Maxwell himself and if there is one person to blame Iâd put it at Helmholtzâs doorstep for his erroneous assertion that Weber electrodynamics violate the conservation of energy. This had the effect of dissuading Maxwell from pursuing an explanation of EM waves in terms (as Maxwell had previously been disposed to do) that comport with Weberâs application of his electrodynamics to telegraphy: The first time the speed of light as we now understand it appeared in engineering. Therefore Maxwellâs monumental work was published under that assumption. Heaviside merely followed the consequences of Maxwellâs damning Weber with faint praise in âA Dynamical Theory of Electromagnetic Fieldâ.
One of several places where people get confused is Maxwellâs use of quaternions to formulate his original 20 equations. To the best of my knowledge, Maxwell used quaternions in a degenerate manner â by which I mean they were in no way isomorphic with 4-vector representations now used in special relativistic electrodynamics. Indeed, one cannot, to the best of my knowledge, formulate Maxwellâs equations in a special relativistic manner without going to bi-quaternions which Maxwell did not use. I qualify these statements because Iâd be happy to see a pure quaternion formulation of special relativistic electrodynanmics or, for that matter, of longitudinal waves.
In using the phrase âspecial relativistic electrodynamicsâ Iâm really just following the logic of Maxwellâs published equations which implied special relativity before the MichelsonâMorley experiment let alone Einstein. Einstein adorned and elaborated Maxwell â so to the extent Einstein was wrong, one can blame Maxwell, except for the vigorous PR campaign the elevated Einstein to the status of Zeus in the pantheon of modern physics â but thatâs another tale of woe we are now living through: The retreat from science to theocracy during the 20th century thatâs all-too-apparent now.
So you have to understand that in my working hypothetical world where fringe physics is true â where classically observable MVP effects are real â special relativity is wrong.
The key to my reviving experimental work is that the theory that I came up with to make my mathematical model of the scope traces match required that I find a theory in which the Coulomb field (scalar potential) is ârigidâ (ie: the electric potential does not âpropagateâ but instantly appears as changed in all points in space simultaneously when a charge âmovesâ) â or at least moves at speeds vastly in excess of the speed of light.
Weber Electrodynamics filled the bill except that there was no developed theory of EM waves in those terms. Andre Assis â the primary proponent of Weber â claimed to have such a theory based in some sense on Weberâs original engineering equations for telegraphy but I wasnât able to locate it. What I was looking for was something like that and finally located a guy at NASA who had some floppy disks stored off somewhere that attempted to describe EM waves in terms of something like the Dirac Sea of charge pairs â which is what I suspected would be necessary to make Weber work. He dug that stuff out and sent it to me, but it wasnât in a form that would permit me to reformulate my model that simply assumed and somehow the above criterion would be met by such an âaetherâ.
However, there has been, in the last few years, an resurgence of interest in Weber Electrodynamics by folks who are coming to understand that the key problem to solve is EM propagation. Once that is solved, we can proceed to address reformulation of QM hence Aharonov Bohm.
2 Likes
Wow, thanks for that reply. You really did cut to the crux of the matter when you mentioned âlongitudinal wavesâ. Thatâs what began my journey, however you soon come to find that itâs an oversimplification of what might actually be occurringâŚwhich is why I refrain from using the word when engaging others for the first time.
I am familiar with Weber electrodynamics, but havenât delved in deeply to it. Iâll check it out again.
As you were eluding to, there are two potentials yes? The Magnetic Vector Potential and the Electric Scalar potentialâŚIâm still unclear on what physical manifestation illustrates the Scalar potentialâŚI guess that one hasnât been experimentally verified as ârealâ yet.
Just curious, are you familiar with the Electromagnetic Missile Effect? Here are some papers on it.
I feel like this particular effect isnât widely understood or even known about. But seems significant as it deals with hyperbolic acceleration of charge gradients at the interface of the antenna and free spaceâŚwhich would involve the âacceleration fieldâ of the MVP and apparently this extends what is considered the Fresnel Near Field region of the antennaâŚwhich I believe can then be used as some type of âvirtual waveguideâ for the energy itself. However, I may be misconstruing this in some way.
Going to take my time and re-read the things that youâve written in your last reply. Thanks again!
PS, I deleted the first post and re-posted because I forgot to âreplyâ to your last message and I wanted it to ping you. But then when I went back to post, it said that it was too similar to my last post! So thatâs why Iâm adding more text here.
PSS not sure why my first link is showing as brokenâŚbut you can find that study easily on google scholar!
2 Likes
On the contrary, there is no controversy over the physical reality of the scalar potential as there is with the vector potential. Where some confusion may arise is in the term âscalar wavesâ which people use as almost synonymous with âlongitudinal wavesâ.
This is because what I humorously call âThe Crackpot Termâ of longitudinal waves is a gradient of a scalar potential that only âcrackpotsâ like yours truly do not exclude from plausible physical reality on the basis that it violates special relativity. That âcrackpotâ scalar potential term is:
v ¡ A
which has the same physical dimensions as the static electric potential aka Coulomb potential aka scalar potential aka ÎŚ. (The âvâ is the same v appearing in the Lorentz force.)
Never heard of it. Iâm deep into getting my version of an experiment designed such that is cheap and simple enough that the usual reasons to ignore experimental results (âNot another lone youtube crackpot with too-many-moving-parts claiming to be âEinsteinâ!â) will not obtain. No time for distractions beyond my physical needs.
2 Likes
Gotcha, thanks for the clarification and good luck!
1 Like
John Denkerâs exposition of electromagnetism using Geometric Algebra (real-valued Clifford Algebra on a (+,+,+,-) signature space) lays things out more clearly â yet without simplification â than any other reference I have found.
The bivectors, planes of rotation, xy, xz, yz are the same as the i, j, k of quaternions.
On a less rarefied level, my Physical Units Factor Tables are a big help in keeping units straight, and fellow Triple Niner Alan Eliasenâs Frink, (online version) is great for practical calculations.
2 Likes