The filaments of incandescent lamps will instantly oxidise and burn through if operated in air. Early Edison bulbs were evacuated to vacuum, but modern bulbs are typically filled with inert argon gas at a pressure of around 70% of sea level atmospheric pressure, which reduces evaporation of the tungsten filament.
Some higher-power lamps are filled with gaseous nitrogen, which has a higher breakdown voltage than argon and does not react with hot tungsten. But what happens if you immerse a bare filament in liquid nitrogen? Let’s see.
2 Likes
Edison’s photon source shines bright – yet now even cooler!
I wonder why N2 isn’t used to backfill incandescent lamps. It’s cheaper that Ar. Perhaps some undesirable chemistry occurs with the N2?
My guess is that N₂, being a diatomic molecule, has more degrees of freedom than monatomic Ar and consequently is a better conductor of heat. Heat conduction reduces the efficiency of the bulb since it carries heat away from the filament to the envelope. I have heard that high-quality double- and triple-glazed windows are filled with Ar for this reason, and the same would apply to incandescent lamps.
Nitrogen does not react with tungsten at these temperatures. Some high-intensity bulbs (for example, projection bulbs) are filled with nitrogen because it has a higher electrical break-down voltage than argon and avoids arcing within the filament and conductors. I guess they’re willing to trade thermal efficiency to avoid that trouble.
Argon is more costly than nitrogen but still relatively inexpensive since it is produced as a by-product of air liquefaction and has a substantial industrial market for applications such as metal-inert-gas (MIG) welding. Around 700,000 tonnes are produced every year worldwide. Heavier noble gases would be even better for filling lamps (not only lower conduction but less evaporation of the filament), but they are far more expensive. Apparently, some special application bulbs are filled with krypton.
The filament in liquid nitrogen trick works because the filament is surrounded by a constantly-refreshed layer of gaseous nitrogen that allows it to heat without being quenched by the liquid nitrogen, kind of like an inverse Leidenfrost effect.
More degrees of freedom means higher specific heat but does not affect the thermal conductivity. In any case, thermal transfer in a light bulb is convective and radiative, not conductive. Thermal conductivity in gases might be relevant in windows, though I’d expect convection to dominate there too.
There are few instances in gases where thermal conductivity is of much importance because gases can transport heat advectively, i.e., by moving around. Thermal conductivity is a transport effect like diffusion. If a woman with heavy perfume enters a room, you’ll smell it within minutes. If diffusion were the only method of transport of the perfume, it would take months to fill the room.
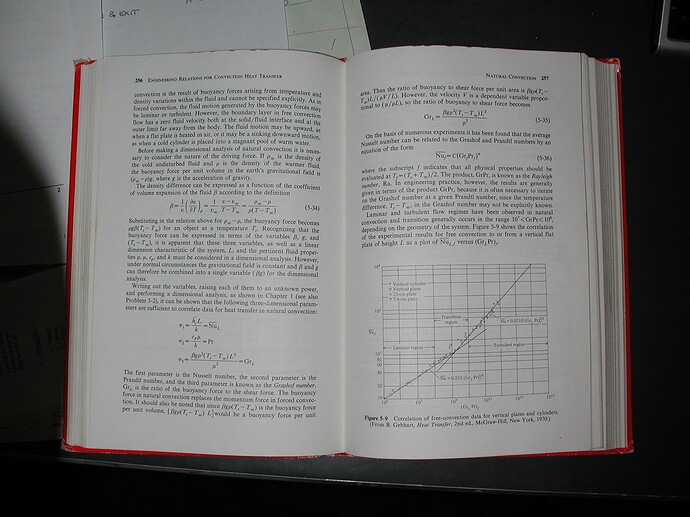
Fluid dynamicists love their dimensionless numbers to characterize these things. The Nusselt number is the ratio of the convective to conductive thermal transfer, which in turn is computable from the Rayleigh number, itself the product of the Grashof number and the Prandtl number. I used to tease my fluid dynamics colleague about all those numbers but he didn’t always find it that funny.
2 Likes
This is what the Wikipedia article on “Insulated glazing” has to say about “Fill gas”.
An older-established way to improve insulation performance is to replace air in the space with a lower thermal conductivity gas. Gas convective heat transfer is a function of viscosity and specific heat. Monatomic gases such as argon, krypton and xenon are often used since (at normal temperatures) they do not carry heat in rotational modes, resulting in a lower heat capacity than poly-atomic gases. Argon has a thermal conductivity 67% that of air, krypton has about half the conductivity of argon. Argon is almost 1% of the atmosphere and isolated at a moderate cost. Krypton and xenon are only trace components of the atmosphere and very expensive. All of these “noble” gases are non-toxic, clear, odorless, chemically inert, and commercially available because of their widespread application in industry. Some manufacturers also offer sulfur hexafluoride as an insulating gas, especially to insulate sound. It has only 2/3 the conductivity of argon, but it is stable, inexpensive and dense. However, sulfur hexafluoride is an extremely potent greenhouse gas that contributes to global warming. In Europe, SF₆ falls under the F-Gas directive which ban or control its usage for several applications. Since 1 January 2006, SF₆ is banned as a tracer gas and in all applications except high-voltage switchgear.
In general, the more effective a fill gas is at its optimum thickness, the thinner the optimum thickness is. For example, the optimum thickness for krypton is lower than for argon, and lower for argon than for air. However, since it is difficult to determine whether the gas in an IGU has become mixed with air at time of manufacture (or becomes mixed with air once installed), many designers prefer to use thicker gaps than would be optimum for the fill gas if it were pure. Argon is commonly used in insulated glazing as it is the most affordable. Krypton, which is considerably more expensive, is not generally used except to produce very thin double glazing units or extremely high performance triple-glazed units. Xenon has found very little application in IGUs because of cost.
Vacuum technology is also used in some non-transparent insulation products called vacuum insulated panels.
So, if this it to be believed, the lower heat capacity (and greater density) of argon compared to air or nitrogen lowers thermal conductivity because “Gas convective heat transfer is a function of viscosity and specific heat.”
This would presumably be the same inside a light bulb and a double-pane window.
This is not correct because the dimensions and thermal gradients are very different. That’s where all those fluid dynamics numbers I mentioned come into play. Without bothering to do the calculation, I’m going to claim that the Nusselt number for a light bulb is much greater than unity, which means that thermal convection dominates over conduction. You can rely on experience for confirmation: the “heat waves” above a hot surface (e.g., asphalt in the summer) are visual evidence of convection at work. The Grashof number is proportional to the temperature difference.
I’ll speculate that the reason there is an “optimum thickness” for the window mentioned in the Wikipedia article is precisely for this reason, i.e, that if the spacing of the panes is too great, viscosity is not high enough to prevent the onset of natural convection.
The Grashof number is inversely proportional to the square of the kinematic viscosity, which is itself inversely proportional to the density. That means the Grashof number is much larger for krypton than it is for argon, for example. Since the Nusselt number is monotonically increasing with Grashof number (see figure below), convection is easier to get going krypton. Once there is convection, thermal transfer is greatly enhanced.
It is left as an exercise to the reader to compute the optimum thickness as a function of gas fill. Too thin and thermal conduction is greater than it need be; too thick and there is free convection. The figure below gives the connection between the Grashof and Nusselt numbers.
1 Like