Problematic Probabilities—Bertrand's Paradox

SCANALYZER Tracking with Closeups
, ,
1

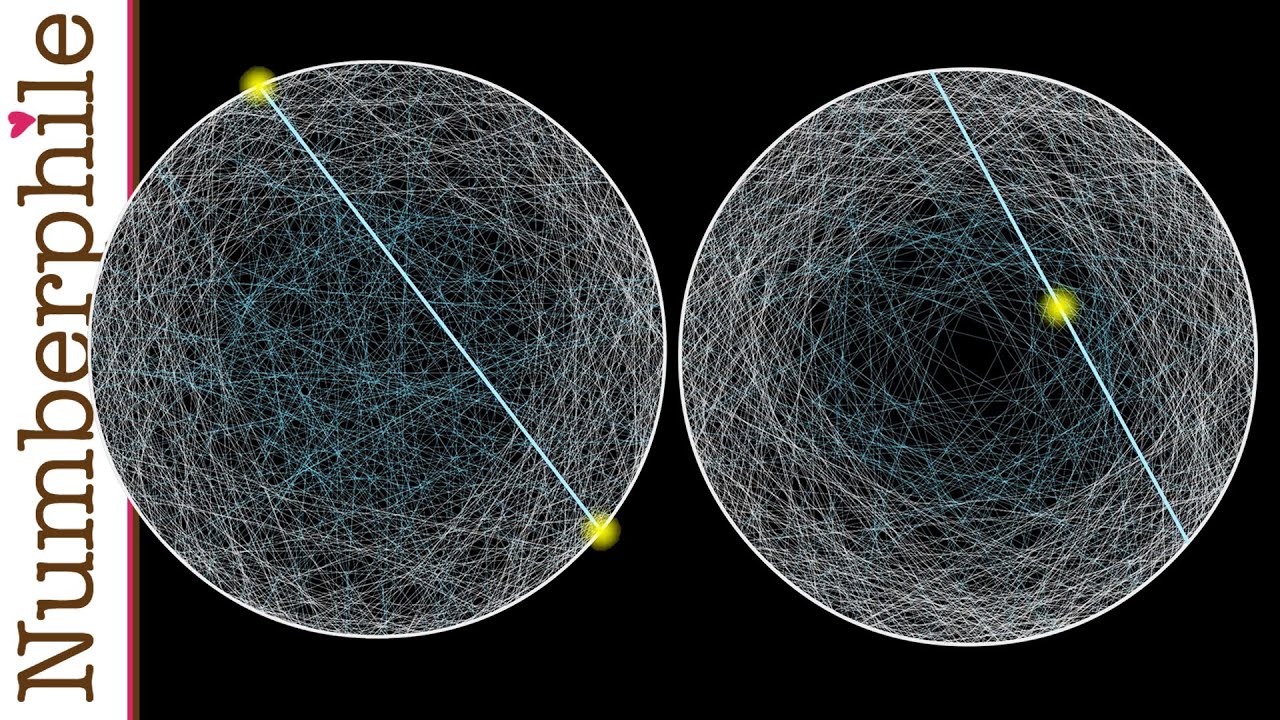
What is the probability a random chord drawn across a circle will be longer than the sides of an equilateral triangle inscribed within it? This is easy to state, and almost as easy to “solve”, until you ask “what do you mean by ‘random’ ”? This is the Bertrand Paradox, which illustrates how difficult is can be to define probabilities when the domain of possibilities is infinite. Here is a deeper dive into Bertrand’s Paradox and the issues behind it.

This is similar to the problem of randomly picking a point on a sphere, where many of the most obvious “methods” produce results that are visibly incorrect.

3 Likes
2

Thanks for this. Totally Fascinating!

A great example of how difficult it can be to pose a question in an unambiguous form.

2 Likes
3

Unlike his examples in the latter part of the first video, the distribution function for choosing the ‘random’ chord is I’ll defined. Of course, it’s not apparent when the problem is initially posed but the first distribution function (uniform points on the circle) is most natural. The other two choices are untethered from points on the circle, though they are defensible choices.

1 Like