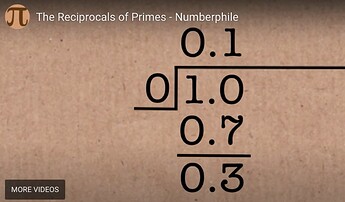
William Shanks is best known for computing entirely by hand, in 1873, the decimal expansion of π to 707 digits (of which the first 527 were correct—the goof was not found until 1944 in a recomputation with a mechanical desk calculator). Between 1876 and 1879, he computed the periods of the repeating decimal representations of the reciprocals of prime numbers between 60,000 and 110,000. Without ever answering the question of why? (which rarely occupies the mind of a recreational mathematician), what does this mean and how might he have done it?
To my knowledge, Shanks never described the mechanism he used to compile his table of primes (2 through 60,000) and primes and reciprocals (60,001 through 110,000). However, it is highly probable that he used the Sieve of Eratosthenes to find the primes in his tables, as that was the method of choice for finding primes in bulk prior to mechanical aids to computation. Known since antiquity, the sieve method requires only addition and enough paper to mark all of the numbers (or, in practice, all the odd numbers) in the desired range.
Here is how the Sieve of Eratosthenes finds all of the primes smaller than 900.
To find the primes less than 60,000, you only need to check off potential factors up to 243 (\sqrt{60000}<245). It does take a lot of paper and crossing out, but it’s vastly less work than trial division.
