Here is Fourmilab’s “Slide Rule” page, exploring the genius of and solving real-world problems with this amazing add-a-log computer. You can follow along with this virtual slide rule that runs in your browser. The Cold War even gave us the Strangelove Slide Rule, a circular pocket computer for estimating the effects of nuclear weapon detonations.
Logarithms are an amazing invention. Or discovery. Irrespective of that, what would have to had been true for ancient greeks to invent (or discover) logarithms?
Ancient Babylonians had something like the logarithm in place. Fascinating to learn that in modern times it has been used in digital arithmetic integer multiplication.
The answer is math… now, what was the question?
ADAMS, Douglas : Nomography Theory and Application(Archon Books,1964, 207 pp. 16MB PDF)
(not that Douglas Adams)
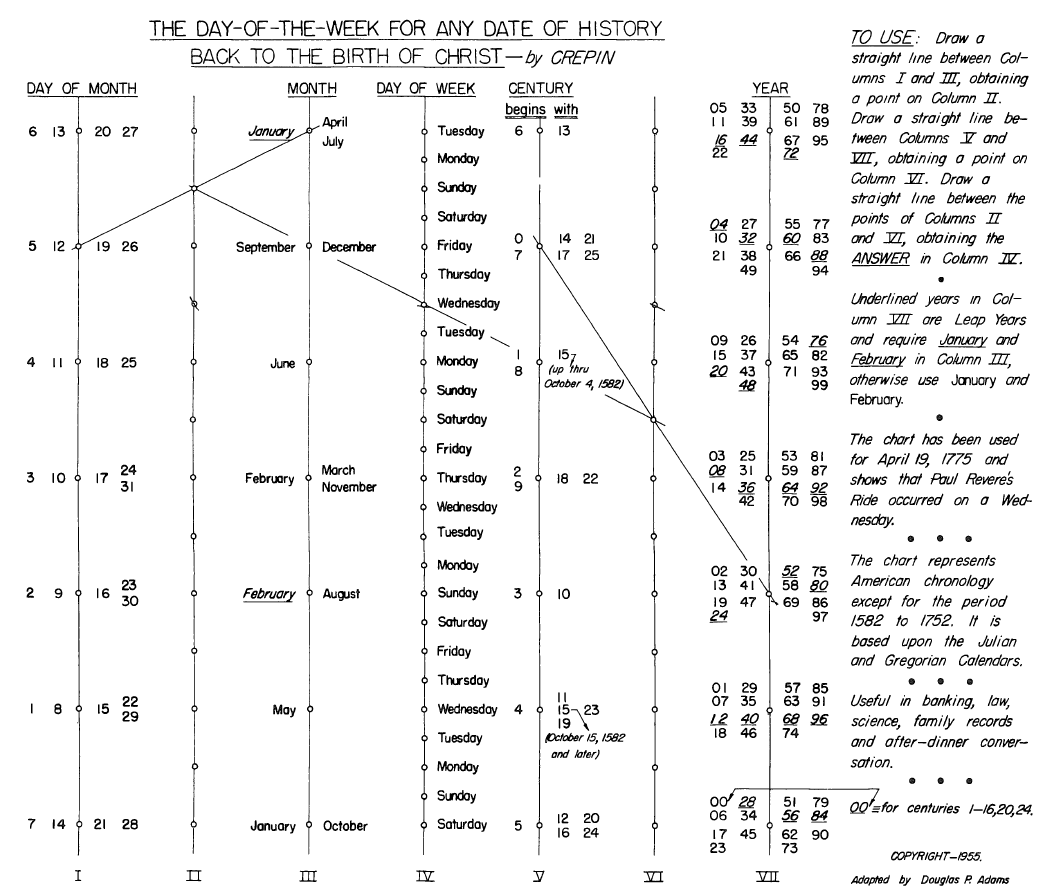
Nomographs or nomograms are basically similar to slide rules, but one uses a free straightedge moved over scales that remain fixed rather than a captive but movable indicator line and scales. Here’s an example:
This book even has a chapter on nomographic electronic computation, which is quite quaint, though somewhat digital - pulse-width modulation on film, as far as I can make out.
The Wikipedia page on nomograms linked above links to some good basic articles and to open-source software for creating nomograms. (It also references the Kolmogorov–Arnold representation theorem, which souds very interesting and useful for machine learning, but I’m not sure what it’s relevance to nomograms is.)
The implication of this theorem is that every function can be represented with a nomogram. Of course, that’s largely of theoretical value.
I think it’s a little more subtle than that, something like: any function of two variables can be represented by a basic nomogram, functions of up to seven variables can be represented with a chained sequence of basic nomograms making up a complicated nomogram, and higher numbers of variables will require special techniques, or possibly solving one of Hibert’s unsolved problems. [or something like that]