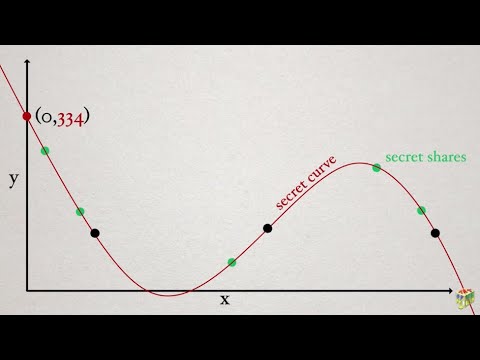
The Shamir Secret Sharing algorithm seems almost magical. It allows you to split a secret (for example, an encryption key, the password for a root signing certificate, or a cryptocurrency private address) into n parts, from which any k, k ≤ n, are sufficient to recover the secret. This allows flexible and secure custodial arrangements where, for example, the password to authorise large money transfers is entrusted to five corporate officers, three of whom must provide their shares in order to reconstruct the complete password.
This video explains how it’s done, which is based upon the Lagrange interpolation theorem, in which k points uniquely define a curve of degree k−1 (and that fewer than k points can be fit by an infinite number of curves of that degree). By encoding the secret as a solution to the unique curve, any k points randomly chosen on the curve suffice to define the polynomial for the curve, whose solution is the secret.
The Multiple Key Manager in Fourmilab Blockchain Tools uses this method to create multi-part shares for Bitcoin and Ethereum private addresses. A description of how this works may be found in the Blockchain Tools User Guide [PDF], section 2.3, starting on page 11.