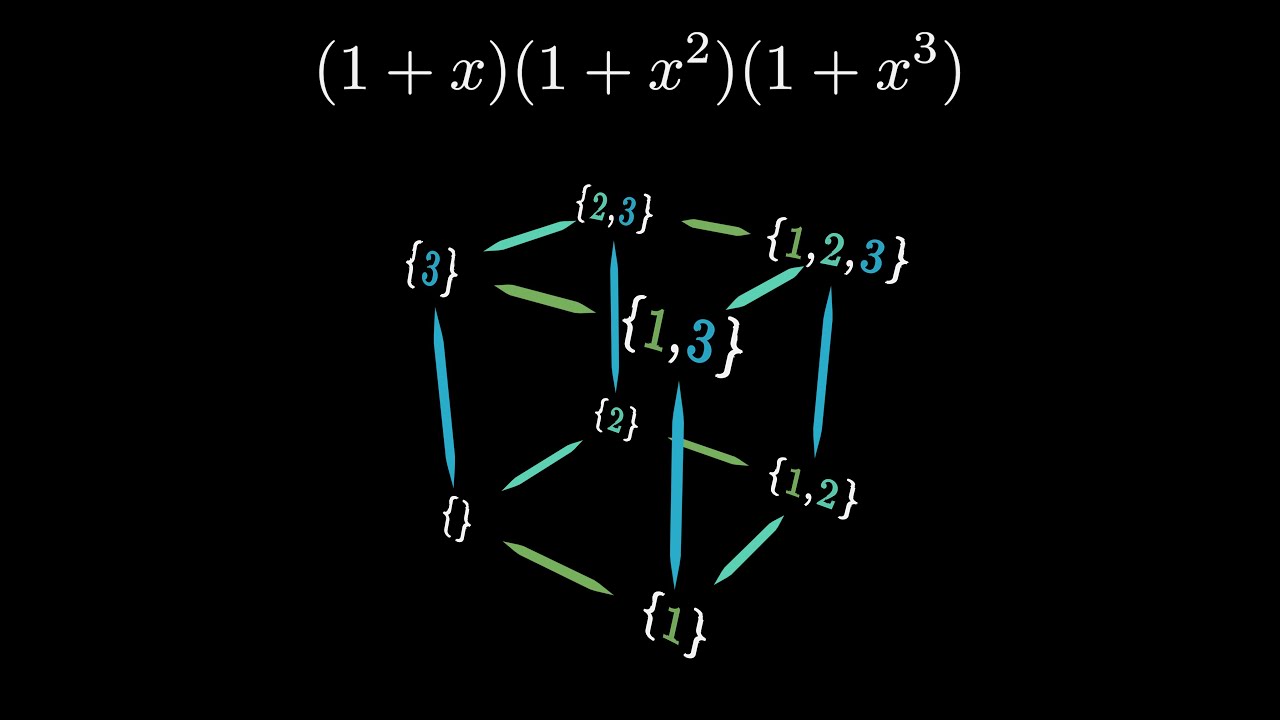
A training problem for International Math Olympiad asks:
Find the number of subsets of \{1,2,3,4,5,\ldots,2000\}, the sum of whose elements is divisible by five.
Easy, right? Just write a program to enumerate all of the subsets of the 2000 element set, add up their members, divide by five, and count the ones with a remainder of zero. You scribble down the program, set it running, and wait for the answer. And wait. And wait. And wait. What’s wrong—did you goof and write an infinite loop? No, but you might as well have done. There are 2^{2000}\sim 10^{500} subsets of a 2000 element set, so if every elementary particle in the visible universe were a supercomputer checking a trillion subsets per second, it would take around 3\times 10^{400} years to check them all, which is rather longer than the present age of the universe, 13.8\times 10^9 years.
So, it is impossible? Not so fast (or so slowly). An extremely subtle and powerful mathematical tool called a generating function allows expressing the subsets in terms of a polynomial whose coefficients count the number of terms with various sums. Treating multiplication of complex numbers as vector rotation in the complex plane allows finding the coefficients expressing sums divisible by five, et voilà, out comes the answer.
It is far from obvious why high-order polynomials and complex numbers should have anything to do with a discrete combinatorial problem, but discovering that they do provides another peek into the deep unity of mathematics and how looking at a problem from a different perspective may allow solving problems which seem utterly intractable at first glance.