Google’s DeepMind has announced AlphaGeometry, an artificial intelligence program that solves geometry problems at the level of gold medalists in the International Mathematical Olympiad: “AlphaGeometry: An Olympiad-level AI system for geometry”.
AlphaGeometry is a neuro-symbolic system made up of a neural language model and a symbolic deduction engine, which work together to find proofs for complex geometry theorems. Akin to the idea of “thinking, fast and slow”, one system provides fast, “intuitive” ideas, and the other, more deliberate, rational decision-making.
Because language models excel at identifying general patterns and relationships in data, they can quickly predict potentially useful constructs, but often lack the ability to reason rigorously or explain their decisions. Symbolic deduction engines, on the other hand, are based on formal logic and use clear rules to arrive at conclusions. They are rational and explainable, but they can be “slow” and inflexible - especially when dealing with large, complex problems on their own.
AlphaGeometry’s language model guides its symbolic deduction engine towards likely solutions to geometry problems. Olympiad geometry problems are based on diagrams that need new geometric constructs to be added before they can be solved, such as points, lines or circles. AlphaGeometry’s language model predicts which new constructs would be most useful to add, from an infinite number of possibilities. These clues help fill in the gaps and allow the symbolic engine to make further deductions about the diagram and close in on the solution.
The research paper, published in Nature on 2024-01-17 is “Solving olympiad geometry without human demonstrations” [full text at link]. Here is the abstract.
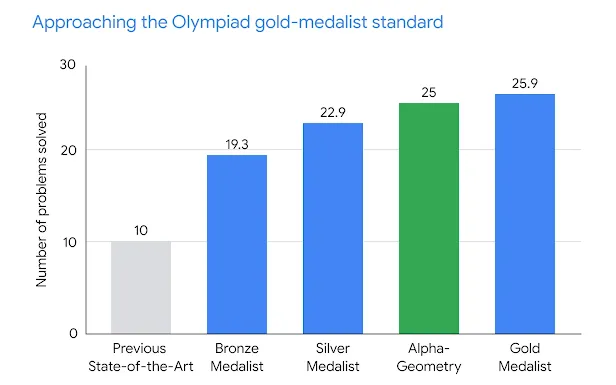
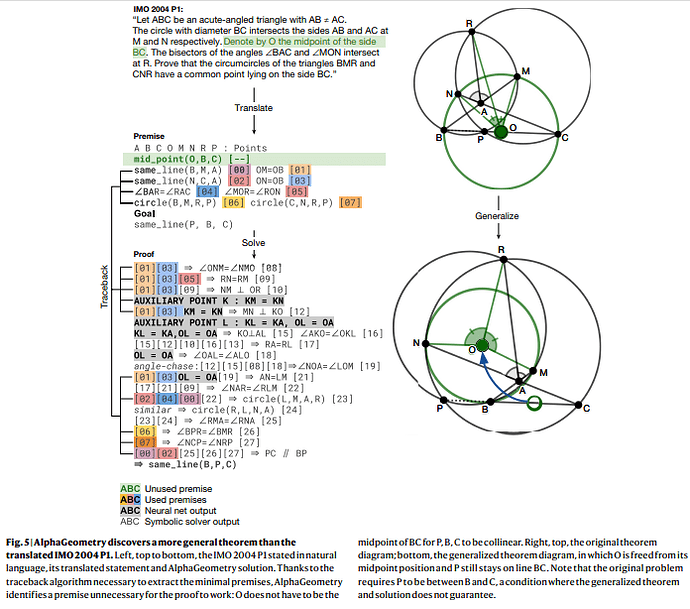
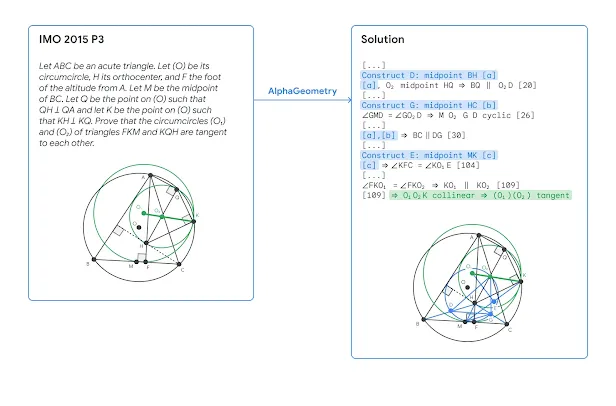
Proving mathematical theorems at the olympiad level represents a notable milestone in human-level automated reasoning, owing to their reputed difficulty among the world’s best talents in pre-university mathematics. Current machine-learning approaches, however, are not applicable to most mathematical domains owing to the high cost of translating human proofs into machine-verifiable format. The problem is even worse for geometry because of its unique translation challenges, resulting in severe scarcity of training data. We propose AlphaGeometry, a theorem prover for Euclidean plane geometry that sidesteps the need for human demonstrations by synthesizing millions of theorems and proofs across different levels of complexity. AlphaGeometry is a neuro-symbolic system that uses a neural language model, trained from scratch on our large-scale synthetic data, to guide a symbolic deduction engine through infinite branching points in challenging problems. On a test set of 30 latest olympiad-level problems, AlphaGeometry solves 25, outperforming the previous best method that only solves ten problems and approaching the performance of an average International Mathematical Olympiad (IMO) gold medallist. Notably, AlphaGeometry produces human-readable proofs, solves all geometry problems in the IMO 2000 and 2015 under human expert evaluation and discovers a generalized version of a translated IMO theorem in 2004.
DeepMind has released complete source code and the trained model as open source: you can download it from GitHub.