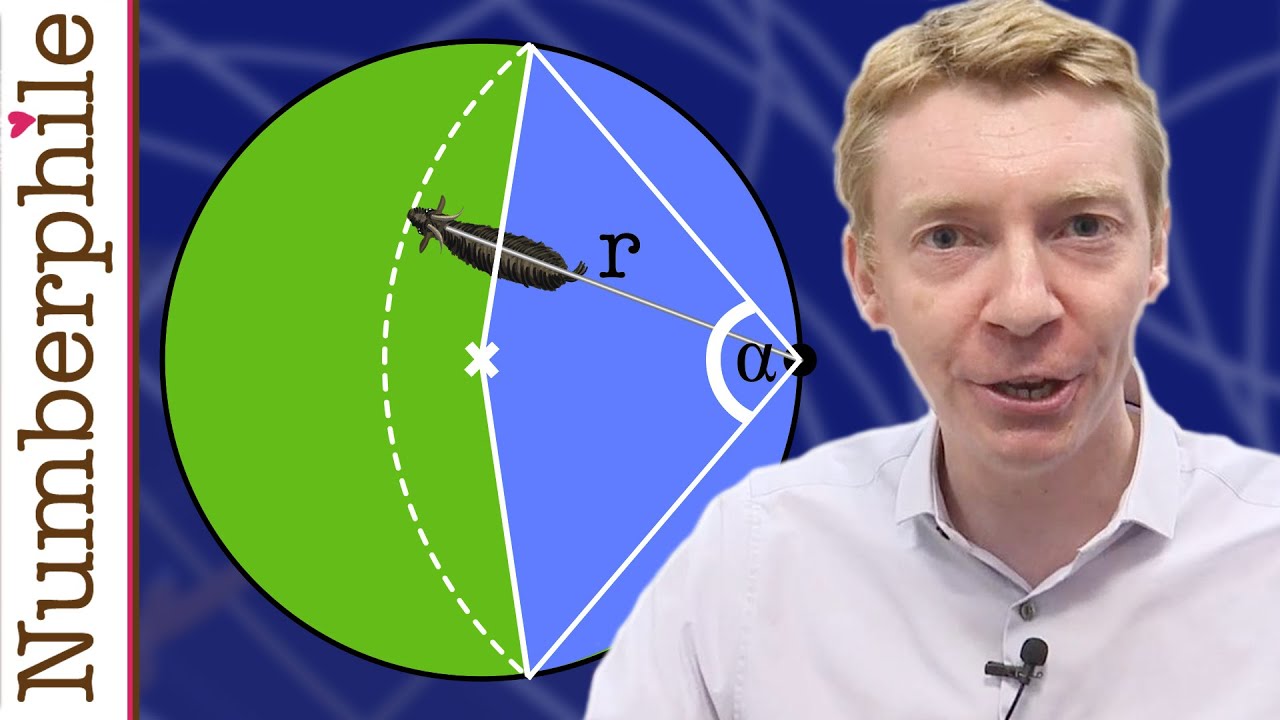
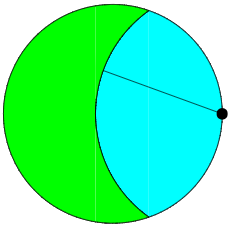
The Goat Problem

SCANALYZER Context
, , ,
1

The goat problem, first formulated in 1894, asks one to calculate the length of a tether by which a goat is attached to the inner circumference of a circular field of unit area, allows the goat to graze exactly one half of the area of the field.

goat

An equation for the radius r of the tether can be obtained by relatively straightforward trigonometry as:

{\frac {1}{2}}\pi =r^{2}\arccos \left({\frac {1}{2}}r\right)+\arccos \left(1-{\frac {1}{2}}r^{2}\right)-{\frac {1}{2}}r{\sqrt {4-r^{2}}}

This is a transcendental equation, which has no closed-form solution, and thus r must be approximated by iteration. Performing this computation yields the approximation of 1.15872847….

The goat problem has long been used an example of a problem which is simple to state, straightforward to solve, yet whose exact solution cannot be written out in terms of simple mathematical operations and functions and must be solved numerically. But in 2020, Ingo Ullish published “A Closed-Form Solution to the Geometric Goat Problem” (behind Springer paywall, jailbreak on Sci-Hub here), in which he used complex analysis to obtain the following closed-form solution as the ratio of two contour integrals in the complex plane:

r=2\cos \left({\frac {1}{2}}{\frac {\oint _{|z-3\pi /8|=\pi /4}z/(\sin z-z\cos z-\pi /2)\,dz}{\oint _{|z-3\pi /8|=\pi /4}1/(\sin z-z\cos z-\pi /2)\,dz}}\right)

Now, some may quibble whether this is a closed-form solution since, in practice, the contour integrals themselves must be evaluated iteratively, most efficiently by a fast Fourier transform.

Interestingly, the goat problem generalised to dimensions greater than 2 is simpler, and has closed-form solutions which, as the number of dimensions goes to infinity, converge to r=\sqrt{2}.

7 Likes
2

“closed form” is a rather problematic phrase and gets into notions of “proof”. For example, the appearance of a symbol, such a π, for an irrational number is “closed form” in the sense that one avoids the ellipsis in the expression but only because one has avoided expression of the numeric value.

By the same token (pun inevitable) symbols such as “sin” and “cos” imply potentially non-terminating numeric expressions.

The trick of resorting to complex analysis may be the most principled way of addressing such problems, in the sense that sqrt(-1) is a form of unity that appears to underlie any directed, cyclic graph of NOR gates hence computation.

2 Likes