Here is more about dielectric mirrors, which can provide up to 99.999% reflectivity for a narrow band of wavelengths or, for a broadband mirror, over 99.5% of visible light across all wavelengths. (Aluminium has reflectivity around 90% in visible light, while silver is in the 95–99% region depending on wavelength.)
He does a nice job explaining ESR film. I worked for 3M and first saw this material in the mid 90s. Prior to the wide spread use of LED displays, one idea that never took off but never died was to use the film as a “light pipe”. The light pipe could move outside light to anywhere within a building or you could have a light source outside an explosive area and provide lighting without having the hassles of purging light sources.
I later worked for the group that manufactured this film as well as other films that take advantage of this technology such as IR reflective films (reflect the IR and pass the visible), brightness enhancing films that collimate light, and security films that prevent off angle viewing. I did write an internal record of invention that utilized the ESR film as a component to another product. The business didn’t think it would sell so I requested the patent process be discontinued.
If you ever get an opportunity to visit 3M’s Innovation center, the technology exhibit is very well done. The exhibit does a terrific job of explaining how capabilities in multiple technologies can lead to new technology. How does a disposable face mask and sand paper lead to a kitchen sponge?
High efficiency reflection with high bandwidth selectivity has implications for Thermal Photovoltaic energy production. At 40% conversion efficiency (see below) the existing fossil fuel infrastructure might permit radical reduction of grid distribution – depending on the capital cost of the TPV system. Decentralized co-generation with natural gas heating would be a big deal.
“A gold mirror on the back of the cell reflects approximately 93% of the below bandgap photons, allowing this energy to be recycled.”
https://www.nature.com/articles/s41586-022-04473-y
Abstract
Thermophotovoltaics (TPVs) convert predominantly infrared wavelength light to electricity via the photovoltaic effect, and can enable approaches to energy storage1,2 and conversion3,4,5,6,7,8,9 that use higher temperature heat sources than the turbines that are ubiquitous in electricity production today. Since the first demonstration of 29% efficient TPVs (Fig. 1a) using an integrated back surface reflector and a tungsten emitter at 2,000 °C (ref. 10), TPV fabrication and performance have improved11,12. However, despite predictions that TPV efficiencies can exceed 50% (refs. 11,13,14), the demonstrated efficiencies are still only as high as 32%, albeit at much lower temperatures below 1,300 °C (refs. 13,14,15). Here we report the fabrication and measurement of TPV cells with efficiencies of more than 40% and experimentally demonstrate the efficiency of high-bandgap tandem TPV cells. The TPV cells are two-junction devices comprising III–V materials with bandgaps between 1.0 and 1.4 eV that are optimized for emitter temperatures of 1,900–2,400 °C. The cells exploit the concept of band-edge spectral filtering to obtain high efficiency, using highly reflective back surface reflectors to reject unusable sub-bandgap radiation back to the emitter. A 1.4/1.2 eV device reached a maximum efficiency of (41.1 ± 1)% operating at a power density of 2.39 W cm–2 and an emitter temperature of 2,400 °C. A 1.2/1.0 eV device reached a maximum efficiency of (39.3 ± 1)% operating at a power density of 1.8 W cm–2 and an emitter temperature of 2,127 °C. These cells can be integrated into a TPV system for thermal energy grid storage to enable dispatchable renewable energy. This creates a pathway for thermal energy grid storage to reach sufficiently high efficiency and sufficiently low cost to enable decarbonization of the electricity grid.
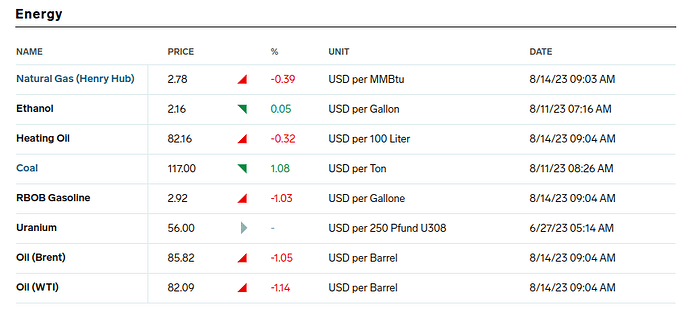
My speculation is that using distinct measurement units provides a slight informational advantage to established players in the commodity markets, which in turn makes it unlikely they would go along with changes just for the sake of consistency.
What I suggested would not require them to go along with anything since all I was suggesting was that there was a market gap* that could be filled simply by someone putting up a website that used SI units.
Or are you suggesting entrenched interests would use something like copyright to kill such a rational move?
*The market I’m thinking of are folks who, like myself, are just wanting to do “back of the envelope calculations” to quickly dispense with wild surmises.
As far as I can tell, converting to SI units would create a rounding problem that would essentially add a layer on top of the market price for each commodity. To me it looks like it would create additional complexity for an unclear upside - what you refer to as back of the envelope calculations.
But I may be wrong.
Have you considered maintaining a spreadsheet that converts to prices in SI units? Copying and pasting fresh data might not be ideal, but it may be an acceptable workaround.
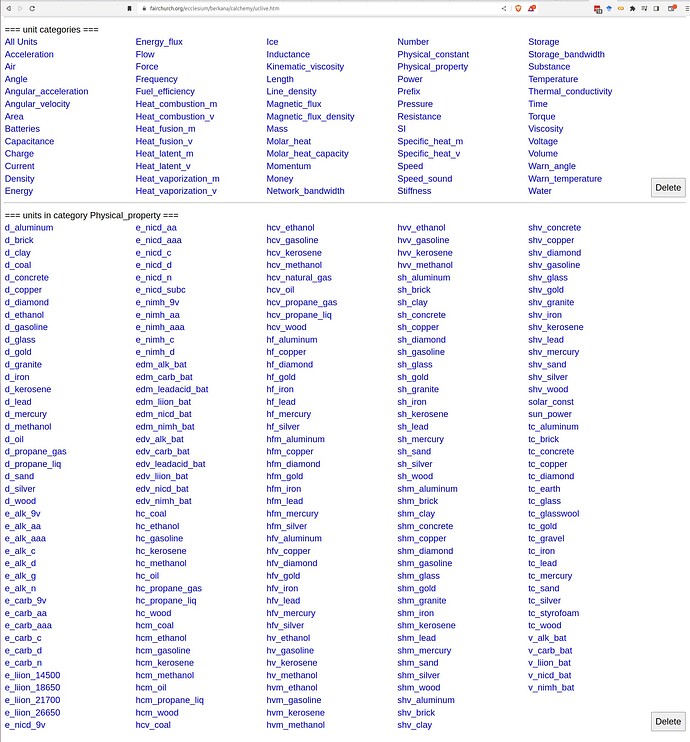
If I were to do such a thing, it would be by extending the “Physical Property” table for Calchemy. For example, I’d just add a constant for MMBtu disambiguated to MMBtuv (v for volume) which, at present, is missing to provide a “back of the envelope” fuel price calculation for TPV cogeneration elex price of <3cents/kWh. On the other hand, there are so many conflicting definitions that I’m not even sure that calculation can be trusted.
Here are the already-existing physical properties supported by Calchemy.
The GNU Units program knows 3523 units, ranging from commonplace to extremely obscure, supports 112 nonlinear units, and common mathematical functions. In 2019, I built a Web interface wrapper, Fourmilab Units Calculator, which adds the ability to define and reference variables used in calculations and automatically updates currency exchange rates and precious metal and Bitcoin prices daily. The link above shows examples of scientific and engineering calculations done with Units Calculator.
I’ve been interested in calculation with physical units for a long time. In 1967, I partially developed an extension to the ALGOL programming language that kept track of units in computations and detected dimensional incompatibility in expressions, and in 1993, patented a similar scheme (U.S. Patent 5,253,193: Computer Method and Apparatus for Storing a Datum Representing a Physical Unit), the story of which, including the original disclosure of the invention and what came out of the sausage machine four years later, is told in “Talkin’ 'Bout My Innovation”.
This gets to the very foundations of metaphysics and is a central piece of my insistence that any programming language solve that problem in more than an ad hoc – let’s tack this onto “type theory” – manner. This is just one more risible gap in high value aspects of society pointing to the occult corrupting influences of the way money enters the economy.
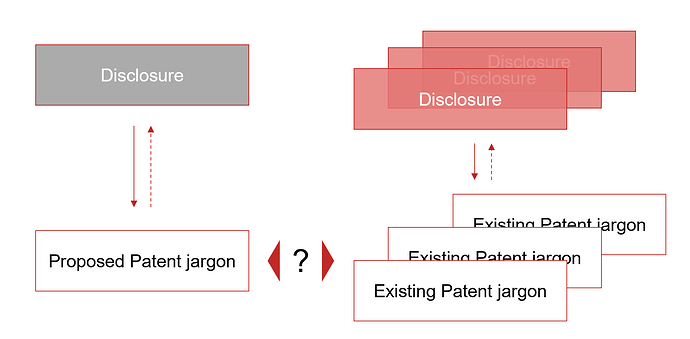
In defense of patent examiners, it’s not an easy job. When they review a proposed new patent, the prior art necessarily includes existing patents, which obfuscate the description of the original disclosures. So while a patent attorney has visibility of both a disclosure and proposed patent, an examiner can only infer the specifics of the invention disclosure, informed or course by experience and professional training.
I’ve sketched a diagram explaining the difficulty of the task confronting an examiner. S/he would trace back the dotted arrow from a proposed patent submission to derive an approximation of the initial disclosure - what is the invention about. Then would compare that against similar approximations for existing patents.
A decision on the merits would be informed by comparing approximations of the original invention disclosures to the disclosure associated with the proposed patent. A new patent submission would typically disclose prior art patents that would - theoretically - ease the job of the examiner, however prior art comparisons are not sufficient to establish whether a proposed patent is new, useful, and non-obvious.
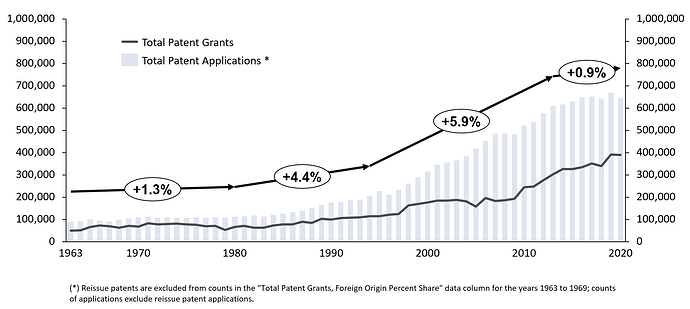
Another aspect related to the work of the examiners has to do with workload. As the business utility of patent portfolios has become more generally accepted the volume of applications has increased significantly. Here is a graph showing trends between 1963 and 2020 (source).
I’ve more or less arbitrarily split the timeline into 4 periods and plotted the CAGR for each in terms of the number of applications
- 1963-1980 … 1.3% CAGR
- 1980-1994 … 4.4% CAGR
- 1994-2013 … 5.9% CAGR
- 2013-2020 … 0.9% CAGR
The big jump in patent applications starting in or about 1994-1995 (Netscape/Web/etc) works out to about a 12 year doubling time - by around 2006, the volume of patent applications had reached 452,000, compared to 206,090 applications in 1994. I find it interesting to speculate as to what technology and business transitions can be retrofitted to support these transitions.
Not shown on the graph, but present in the data source is the split across patent types, as well as a break down by percentage of foreign origin of patents granted. While patent grants with a foreign origin accounted for approximately 20% in the 1960s, by the 2000s, that was hovering around the 50% mark.
Visually, the graph shows an increasing lag between applications and grants, which I believe supports the explanation I offered above: as the volume of applications and grants increases, the complexity of the patent examiner’s work increases as well, which increases the amount of time between when a patent application is submitted to when it is granted.
I could not find historical data in terms of staffing for a period longer than 2008-2016 (source). During that time, the USPTO examiner staff across all technology centers increased from 6,045 to 8,180, with a peak of 8,478 reached in Jan 2015. During the 2008-2016 period, the USPTO received 5.1M patent applications, averaging 567,000 patents annually. So a back of the envelope calculation would indicate an average examiner handles about 80 applications per year. With ~260 working days each year, the USPTO examiner workload is pretty intense.
The USPTO statistics website include a wealth of additional available data sources.
The authoritative source repository is inaccessible, otherwise I’d go in there and see if how hard it would be to add Calchemy’s semicolon operator ‘;’ which says:
Don’t make me reach across they keyboard to hunt for an operator key or even think about what operation to use here … you know what I mean by virtue of the quantities I’ve given you and units that I’ve asked for the answer in terms of. Just do what computers are supposed to do and SOLVE for the operator, 'mkay?
https://www.calchemy.com/sbda.htm
I’m a lazy human and you’re a computer – got it?
Oh, yeah, and if I leave something out just tell me what dimensions I’m off by. And if there is more than one solution, just list them out and let me choose. Can you do that for me? Sure you can. I knew you could!
For about the past 20 years I’ve been using Alan Eliasen’s marvelous physically-typed interpreted language Frink for calculations with units, e.g. specific energy in Earth orbit:
1/2 (3.866 decifurlongs/jiffy)^2 -> centiroods/sq nanofortnight
4.3735817771089920002
Frink is entirely Alan’s work and is free as in beer, but not open source, except for the units file (which has some amusing rants in the comments, e.g. regarding the definition of the lumen). Frink uses unlimited-precision rational numbers by default, but also handles floats, integer, complex and interval math (but not complex intervals). It has extremely fast factoring and other number-theory functions; some of the math routines have been adopted by the main Java math libraries. (Frink is written mainly in Frink but runs on the JVM and has Java introspection.) It can handle any product of SI base units raised to any rational power, and has additional base units for information (bits) and currency (USD, though it can convert to any ISO currency code including XAU and XAG and can adjust for historical values of the dollar and GBP). It has Unicode support throughout - it used to be able to translate languages, even Chinese, until Google translate started charging for API use. Frink is extremely accurate, with unit definitions referring to authoritative standards whenever they exist (not so much for e.g. the many types of cubits), but the date/time math is particularly obsessive about accuracy, accounting for leap-seconds and all sorts of calendrical minutiae.
Frink is remarkably easy to use, including on Android phones. Frink Server Pages allows easily incorporating it into web pages. Frink has some very nice programming features such as arbitrary variable constraints; data structures including arbitrary-dimensional non-rectangular heterogeneous arrays; self-evaluation, regexp, dimensioned graphics and many other conveniences. All the essential Frink documentation is on the first-linked page above - a rather long page .
I use Frink more than any other programs besides browsers and text editors.
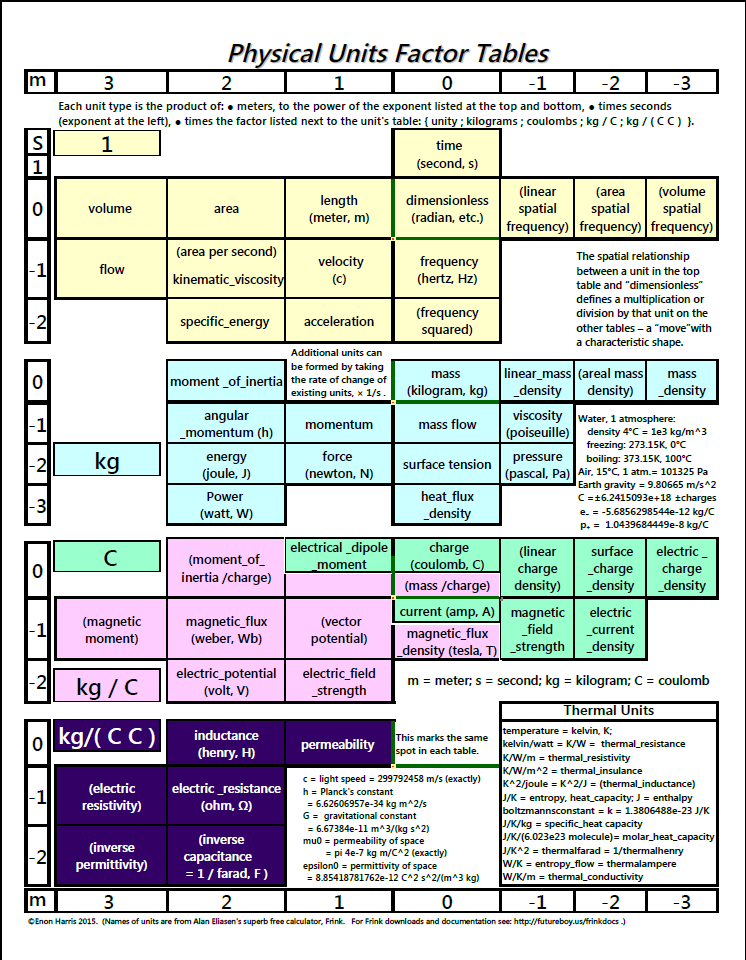
Here is a chart of some of the more important classes of units in Frink. The names in parentheses weren’t official Frink names at the time I drafted the chart, though it could calculate using those quantities.
(PDF version)
(This uses electrical charge (Coulombs) as a base unit rather than the stupid ISO choice of current (Amperes = Coulombs / second) which would mess everything up.)
I wish Wolfram would fix Mathematica’s Quantity system. I reported this bug over a year ago.
FindRoot[{x == Quantity[1, “Seconds”],
y == Quantity[2, “Meters”]}, {{x, Quantity[3, “Seconds”]}, {y,
Quantity[4, “Meters”]}}]
FindRoot::nlu: – Message text not found – ({3.s,4.m}) ({x,y}) ({2.s,2.m}) ({2}) (Removed[$$Failure])
And I just ran into again today trying to duplicate this blog’s calculation of fundamental physical constants in Mathematica:
I use the following a lot while doing work in Mathematica: