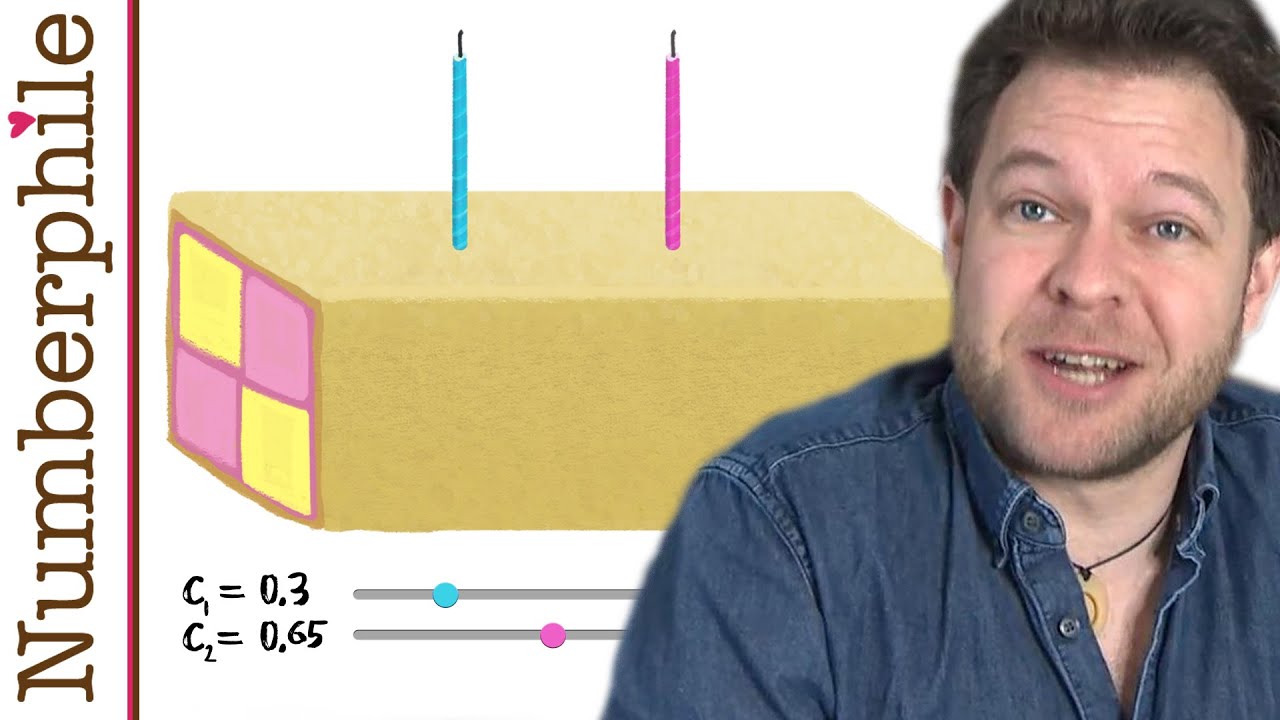
Given a rectangular cake, place two candles along its length at uniformly-distributed random positions. (In a uniform distribution, each candle has an equal probability of being placed at any position along the length.) Now cut the cake into two pieces with a knife at a random position along the length (also uniformly-distributed). What is the probability each piece will have one candle?
Solving this puzzle provides an excellent illustration of how problems in mathematics can be approached from different angles, each providing its own insight on what is going on.
But what if the cake is round and not square? Glad you asked… Now we get into the thorny matter of “Just what do you mean by ‘random’? ”.