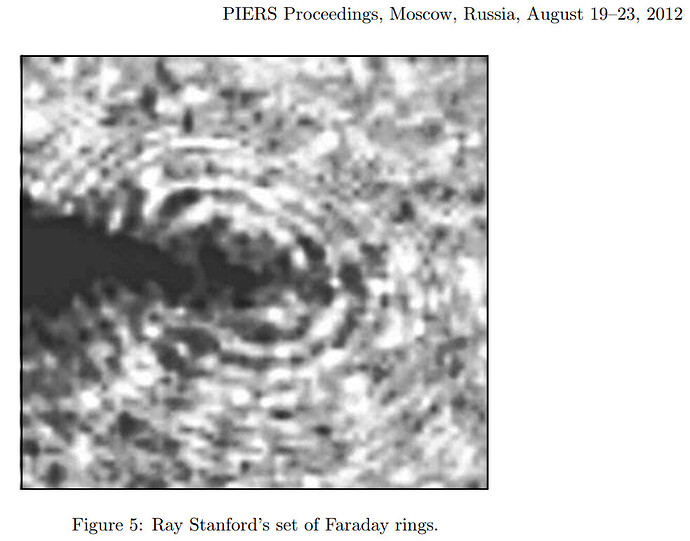
Faraday Effect (DC) rotates polarization in accord with the magnitude of the curl of the MVP=B:
So these “Faraday Rings” can only occur if the current through the center of them is adequate to cause multiple 360degree rotations of the ambient polarization of sunlight – and appear because the magnitude of the curl of the MVP falls off as the CUBE of the radial distance from the current.

From this, we can calculate the B field at distance from the UFO:
Where μ=I*A= amp meters^2=magnetic dipole moment
The video states magnetic dipole moment about 10^11 to 10^13 amp meters^2
Substituting: μ=10^12
The magnetic field (B field) even a football field length away (100m) is 1 Tesla.
4 Likes
Or you could cut to the chase and conclude it’s obvious ringing artifacts from image capture / compression.
3 Likes
It’s reasonable to suspect something is amiss simply on the basis of the strength of the magnetic field at such a distance, but let’s examine your critique to see if it holds up under scrutiny:
If by “ring artifacts” you mean concentric rings like this:
in an interference pattern with a grid – a Miore pattern which appears if one shrinks the rings to the point that sampling frequency approaches screen resolution:

Tracking down the provenance of the “UFO” image:
The rings purportedly show up only at one point in a 25s motion picture taken at 54 frames per second Super 8 Canon camera Dec. 4, 1980 shortly after sunset toward the west.
Questons:
- Where does the ring structure come from? Image searching for various combinations of “compression”, “ring”, “artifact”, “fresnel”, “moire”, etc. turn up no images that match.
- Why is the axis of the elliptical ring structure at an angle?
- Did Ray Stanford lie about the ring structure showing up at only one point in time corresponding to “exactly at the instant where one these objects encountered a long unidentified structure (dark edge in Figure 5)”?
https://www.youtube.com/watch?v=kvON6smO1Aw&t=705s
Here’s visual context:
3 Likes
By ring artifacts I mean the circular light/dark patterns. This is a common artifact in image compression depending on the algorithm.
What sensor does this camera have? Is this RAW format or exported compressed video (TS, h264, etc.)? Are the still frames processed?
You can see examples in optics like this:
3 Likes
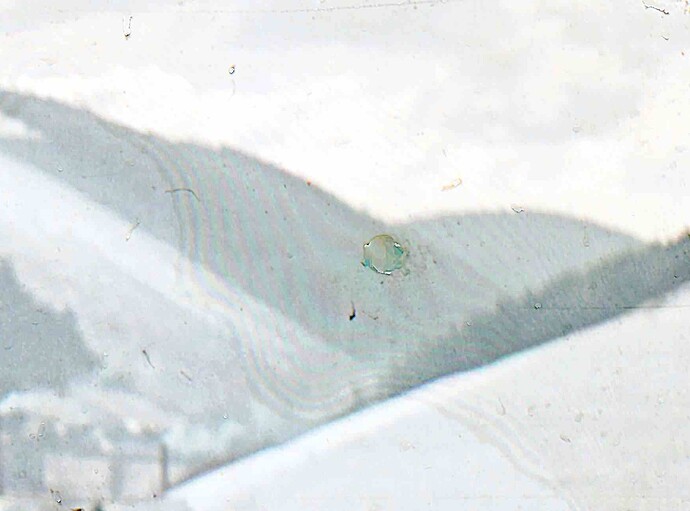
There are other ways to get such rings in photography that have nothing to do with digital compression, screen resolution, or Faraday rotation. Newton’s rings appear as an interference pattern caused by reflections from two optical surfaces of different curvature. Thin films can also produce such a pattern. The link, above has several illustrations of such rings absent any UFOs. The figure below is a cropped version of one of the figures in the link showing such a fringe pattern (as we physicists call 'em).
4 Likes
Assuming the Super 8 Canon film camera as reported in the aforelinked paper all of my questions could be answered:
- Newton’s rings
- n/a (Newton’s rings have no particular expected orientation)
- Newton’s rings, being a thin film defect, are not expected to show up in multiple frames in the same way and indeed may show up in only one frame. So Stanford could just be engaging in motivated reasoning/confirmation bias – perhaps extreme.
Moreover, they would tend to show up in a fresnel-like pattern if due to a point pressure distortion in a thin film, and although it isn’t obviously a diffraction rainbow pattern in the color image, it is plausibly there.
On the other hand Faraday Effect does vary by wavelength so it may produce a rainbow pattern as well.
If it isn’t too hard, maybe I’ll try to model the Faraday Effect in Mathematica of light passing through a dipole to see if the resulting polarization results in something that could plausibly be concentric ellipses. It may be that it can’t even form that shape.
2 Likes
Well this puts the last nail in the coffin of the magnetic field theory:
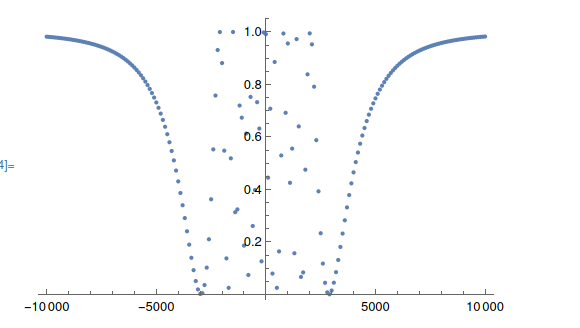
The change in spatial frequency is the opposite of the pattern in the image. Moreover, it is intuitive given the inverse cubed law with distance of the magnetic field around a magnetic dipole since the inverse cube plot looks like:
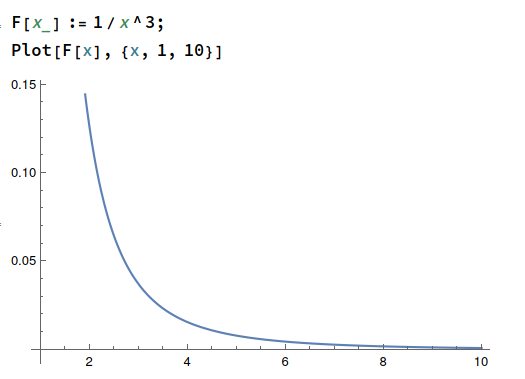
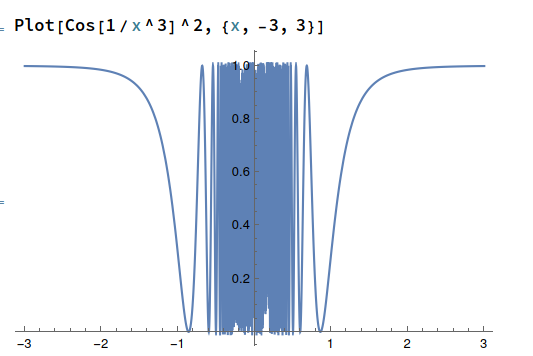
2 Likes